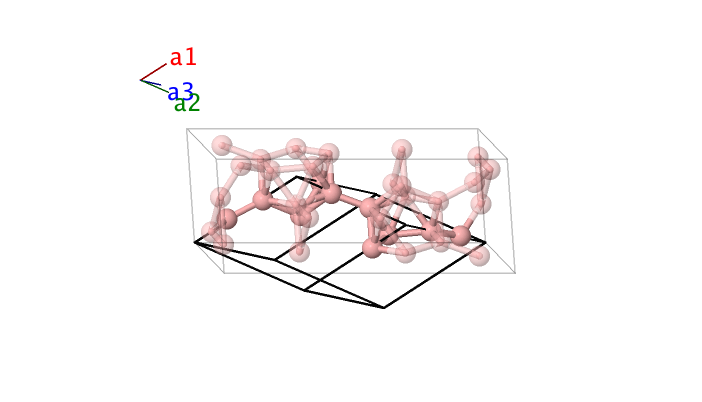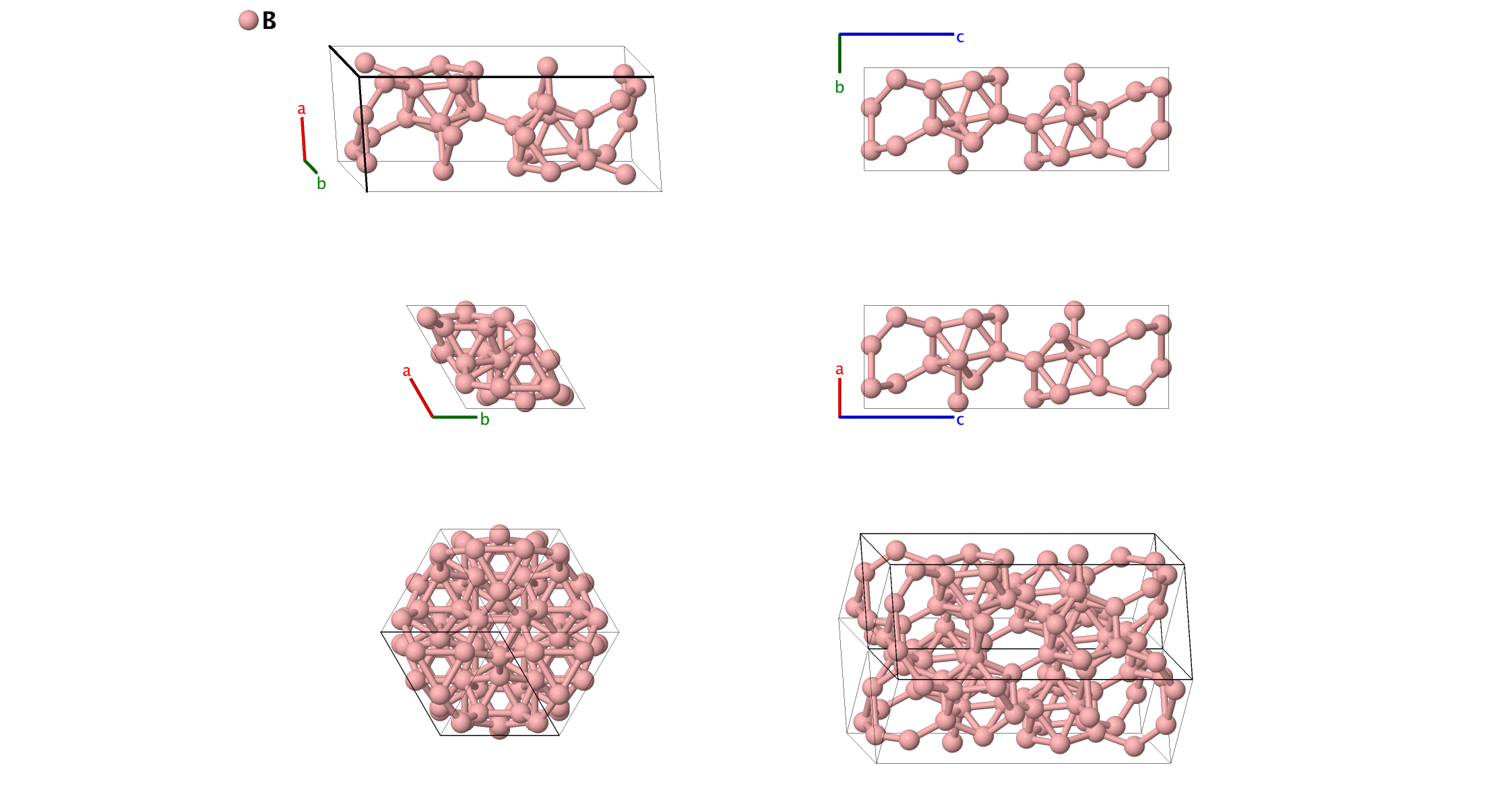
$\alpha$–B (hR12) Structure: A_hR12_166_2h
| Prototype | : | $\alpha$–B |
| AFLOW prototype label | : | A_hR12_166_2h |
| Strukturbericht designation | : | None |
| Pearson symbol | : | hR12 |
| Space group number | : | 166 |
| Space group symbol | : | $\mbox{R}\bar{3}\mbox{m}$ |
| AFLOW prototype command | : | aflow --proto=A_hR12_166_2h [--hex] --params=$a,c/a,x_{1},z_{1},x_{2},z_{2}$ |
- This is a metastable phase of boron, and the simplest known phase (the ground state, $\beta$–B, has 105 or 320 atoms in the unit cell). Note the relationship between the icosahedra in this structure, in T–50 B, and in $\beta$–B. (Donohue, 1982) refers to this as rhombohedral-12 boron. Hexagonal settings of this structure can be obtained with the option ––hex.
Rhombohedral primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & ~ \frac12 \, a \, \mathbf{\hat{x}} - \frac{1}{2\sqrt{3}} \, a \, \mathbf{\hat{y}} + \frac13
\, c \, \mathbf{\hat{z}} \\
\mathbf{a}_2 & = & \frac{1}{\sqrt{3}} \, a \, \mathbf{\hat{y}} + \frac13 \, c \, \mathbf{\hat{z}} \\
\mathbf{a}_3 & = & - \frac12 \, a \, \mathbf{\hat{x}} - \frac{1}{2\sqrt{3}} \, a \, \mathbf{\hat{y}} + \frac13
\, c \, \mathbf{\hat{z}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & =&x_{1} \, \mathbf{a}_{1}+ x_{1} \, \mathbf{a}_{2}+ z_{1} \, \mathbf{a}_{3}& =&\frac12 \, \left(x_{1} - z_{1}\right) \, a \, \mathbf{\hat{x}}+ \frac1{2\sqrt3} \left(x_{1} - z_{1}\right) \, a \, \mathbf{\hat{y}}+ \frac13 \, \left(2 x_{1} + z_{1}\right) \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{B I} \\ \mathbf{B}_{2} & =&z_{1} \, \mathbf{a}_{1}+ x_{1} \, \mathbf{a}_{2}+ x_{1} \, \mathbf{a}_{3}& =&\frac12 \, \left(z_{1} - x_{1}\right) \, a \, \mathbf{\hat{x}}+ \frac1{2\sqrt3} \left(x_{1} - z_{1}\right) \, a \, \mathbf{\hat{y}}+ \frac13 \, \left(2 x_{1} + z_{1}\right) \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{B I} \\ \mathbf{B}_{3} & =&x_{1} \, \mathbf{a}_{1}+ z_{1} \, \mathbf{a}_{2}+ x_{1} \, \mathbf{a}_{3}& =&\frac1{\sqrt3} \left(z_{1} - x_{1}\right) \, a \, \mathbf{\hat{y}}+ \frac13 \, \left(2 x_{1} + z_{1}\right) \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{B I} \\ \mathbf{B}_{4} & =&- x_{1} \, \mathbf{a}_{1}- x_{1} \, \mathbf{a}_{2}- z_{1} \, \mathbf{a}_{3}& =&\frac12 \, \left(z_{1} - x_{1}\right) \, a \, \mathbf{\hat{x}}+ \frac1{2\sqrt3} \left(z_{1} - x_{1}\right) \, a \, \mathbf{\hat{y}}- \frac13 \, \left(2 x_{1} + z_{1}\right) \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{B I} \\ \mathbf{B}_{5} & =&- z_{1} \, \mathbf{a}_{1}- x_{1} \, \mathbf{a}_{2}- x_{1} \, \mathbf{a}_{3}& =&\frac12 \, \left(x_{1} - z_{1}\right) \, a \, \mathbf{\hat{x}}+ \frac1{2\sqrt3} \left(z_{1} - x_{1}\right) \, a \, \mathbf{\hat{y}}- \frac13 \, \left(2 x_{1} + z_{1}\right) \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{B I} \\ \mathbf{B}_{6} & =&- x_{1} \, \mathbf{a}_{1}- z_{1} \, \mathbf{a}_{2}- x_{1} \, \mathbf{a}_{3}& =&\frac1{\sqrt3} \left(x_{1} - z_{1}\right) \, a \, \mathbf{\hat{y}}- \frac13 \, \left(2 x_{1} + z_{1}\right) \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{B I} \\ \mathbf{B}_{7} & =&x_{2} \, \mathbf{a}_{1}+ x_{2} \, \mathbf{a}_{2}+ z_{2} \, \mathbf{a}_{3}& =&\frac12 \, \left(x_{2} - z_{2}\right) \, a \, \mathbf{\hat{x}}+ \frac1{2\sqrt3} \left(x_{2} - z_{2}\right) \, a \, \mathbf{\hat{y}}+ \frac13 \, \left(2 x_{2} + z_{2}\right) \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{B II} \\ \mathbf{B}_{8} & =&z_{2} \, \mathbf{a}_{1}+ x_{2} \, \mathbf{a}_{2}+ x_{2} \, \mathbf{a}_{3}& =&\frac12 \, \left(z_{2} - x_{2}\right) \, a \, \mathbf{\hat{x}}+ \frac1{2\sqrt3} \left(x_{2} - z_{2}\right) \, a \, \mathbf{\hat{y}}+ \frac13 \, \left(2 x_{2} + z_{2}\right) \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{B II} \\ \mathbf{B}_{9} & =&x_{2} \, \mathbf{a}_{1}+ z_{2} \, \mathbf{a}_{2}+ x_{2} \, \mathbf{a}_{3}& =&\frac1{\sqrt3} \left(z_{2} - x_{2}\right) \, a \, \mathbf{\hat{y}}+ \frac13 \, \left(2 x_{2} + z_{2}\right) \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{B II} \\ \mathbf{B}_{10} & =&- x_{2} \, \mathbf{a}_{1}- x_{2} \, \mathbf{a}_{2}- z_{2} \, \mathbf{a}_{3}& =&\frac12 \, \left(z_{2} - x_{2}\right) \, a \, \mathbf{\hat{x}}+ \frac1{2\sqrt3} \left(z_{2} - x_{2}\right) \, a \, \mathbf{\hat{y}}- \frac13 \, \left(2 x_{2} + z_{2}\right) \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{B II} \\ \mathbf{B}_{11} & =&- z_{2} \, \mathbf{a}_{1}- x_{2} \, \mathbf{a}_{2}- x_{2} \, \mathbf{a}_{3}& =&\frac12 \, \left(x_{2} - z_{2}\right) \, a \, \mathbf{\hat{x}}+ \frac1{2\sqrt3} \left(z_{2} - x_{2}\right) \, a \, \mathbf{\hat{y}}- \frac13 \, \left(2 x_{2} + z_{2}\right) \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{B II} \\ \mathbf{B}_{12} & =&- x_{2} \, \mathbf{a}_{1}- z_{2} \, \mathbf{a}_{2}- x_{2} \, \mathbf{a}_{3}& =&\frac1{\sqrt3} \left(x_{2} - z_{2}\right) \, a \, \mathbf{\hat{y}}- \frac13 \, \left(2 x_{2} + z_{2}\right) \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{B II} \\ \end{array} \]References
- B. F. Decker and J. S. Kasper, The crystal structure of a simple rhombohedral form of boron, Acta Cryst. 12, 503–506 (1959), doi:10.1107/S0365110X59001529.
Found in
- J. Donohue, The Structure of the Elements (Robert E. Krieger Publishing Company, Malabar, Florida, 1982)., pp. 57-60.