The Triclinic Crystal System
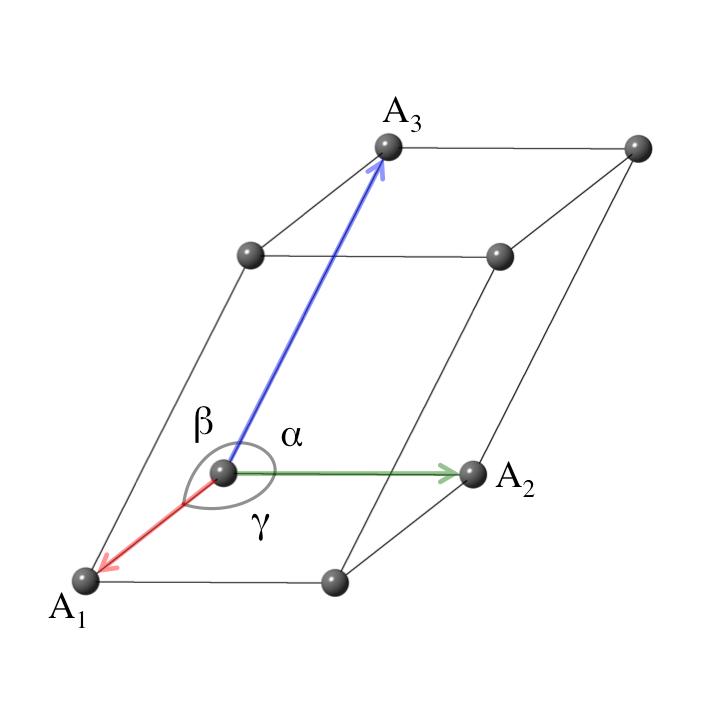
Triclinic is the most general crystal system. All other
crystal systems can be considered special cases of the
triclinic. The primitive vectors are also completely general: their
lengths ($a$, $b$, $c$) and angles ($\alpha$, $\beta$, $\gamma$) may
have arbitrary values. The triclinic system has one Bravais lattice,
which is also the conventional lattice for this system.
Lattice 1: Triclinic
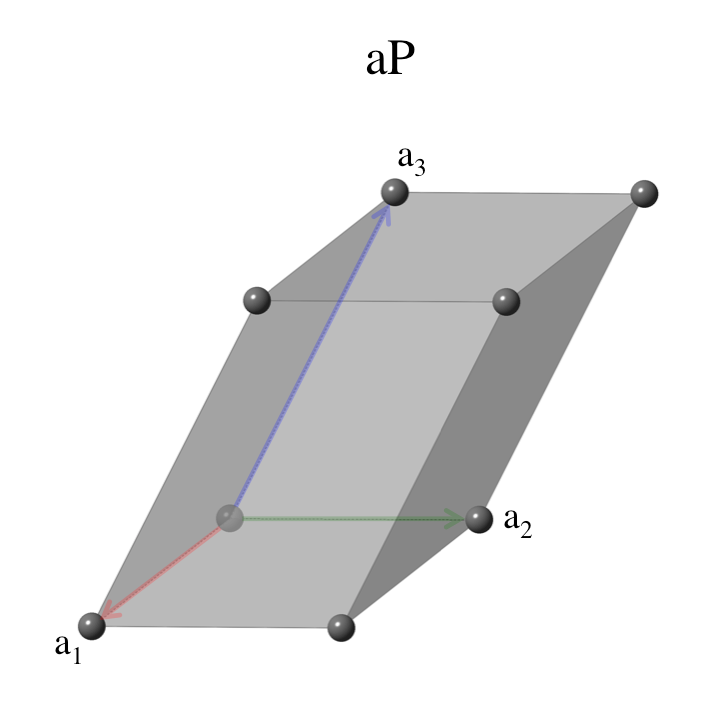
There are many choices for the primitive vectors in the triclinic
system. We make the choice
\[
\begin{eqnarray}
\mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \nonumber \\
\mathbf{a}_2 & = & b \, \cos\gamma \, \mathbf{\hat{x}} + b \, \sin\gamma \,\mathbf{\hat{y}}
\nonumber \\
\mathbf{a}_3 & = & c_x \, \mathbf{\hat{x}} + c_y \, \mathbf{\hat{y}} + c_z \, \mathbf{\hat{z}},
\end{eqnarray}
\]
where
\[
\begin{eqnarray*}
c_x & = & c \, \cos\beta \\
c_y & = & \frac{c \, (\cos\alpha - \cos\beta \, \cos\gamma)}{\sin\gamma}
\end{eqnarray*}
\]
and
\[
\begin{eqnarray*}
c_z & = & \sqrt{c^2 - c_x^2 - c_y^2}.
\end{eqnarray*}
\]
The volume of
the triclinic unit cell is
\[
\begin{equation}
V = a \, b \, c_z \, \sin\gamma.
\end{equation}
\]
The space groups associated with the triclinic lattice are
\begin{array}{ll}
1. ~ \mbox{P1} & 2. ~ \mbox{P}\overline{1} \\
\end{array}