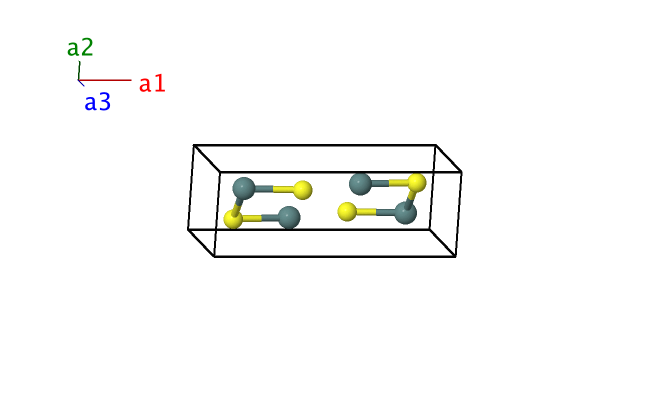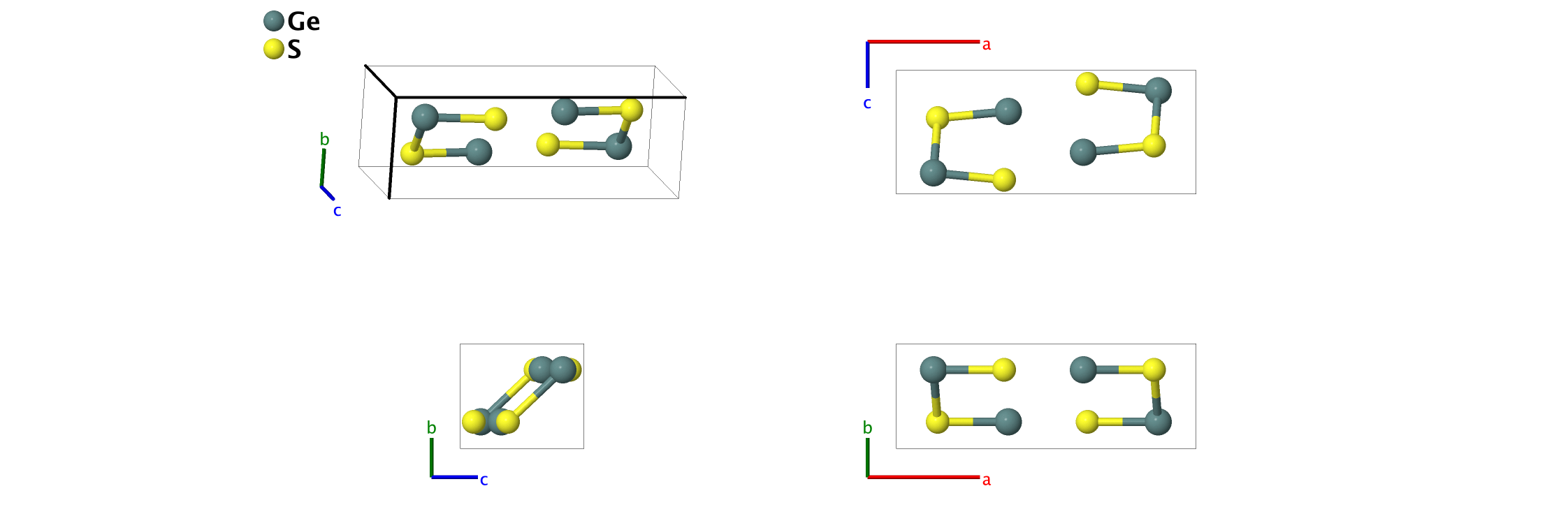
GeS (B16) Structure: AB_oP8_62_c_c
| Prototype | : | GeS |
| AFLOW prototype label | : | AB_oP8_62_c_c |
| Strukturbericht designation | : | $B16$ |
| Pearson symbol | : | oP8 |
| Space group number | : | 62 |
| Space group symbol | : | $\mbox{Pnma}$ |
| AFLOW prototype command | : | aflow --proto=AB_oP8_62_c_c --params=$a,b/a,c/a,x_{1},z_{1},x_{2},z_{2}$ |
Other compounds with this structure
- GeSe, GeS, GeTe, PbS, PbSe, PbTe, SnS, SnSe, SnTe
- Also see the closely related B29 (SnS) structure. (Parthé, 1993) prefers the B16 designation for both structures. Note that GeS (AB_oP8_62_c_c, GeS), MnP (AB_oP8_62_c_c, MnP), FeB (AB_oP8_62_c_c, FeB), and SnS (AB_oP8_62_c_c, SnS) have the same AFLOW prototype label. They are generated by the same symmetry operations with different sets of parameters (––params) specified in their corresponding CIF files.
Simple Orthorhombic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \\
\mathbf{a}_2 & = & b \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \, \mathbf{\hat{z}}
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & =&x_{1} \, \mathbf{a}_{1}+ \frac14 \, \mathbf{a}_{2}+ z_{1} \, \mathbf{a}_{3}& =&x_{1} \, a \, \mathbf{\hat{x}}+ \frac14 \, b \, \mathbf{\hat{y}}+ z_{1} \, c \, \mathbf{\hat{z}}& \left(4c\right) & \mbox{Ge} \\ \mathbf{B}_{2} & =&\left(\frac12 - x_{1}\right) \, \mathbf{a}_{1}+ \frac34 \, \mathbf{a}_{2}+ \left(\frac12 + z_{1}\right) \, \mathbf{a}_{3}& =&\left(\frac12 - x_{1}\right) \, a \, \mathbf{\hat{x}}+ \frac34 \, b \, \mathbf{\hat{y}}+ \left(\frac12 + z_{1}\right) \, c \, \mathbf{\hat{z}}& \left(4c\right) & \mbox{Ge} \\ \mathbf{B}_{3} & =&- x_{1} \, \mathbf{a}_{1}+ \frac34 \, \mathbf{a}_{2}- z_{1} \, \mathbf{a}_{3}& =&- x_{1} \, a \, \mathbf{\hat{x}}+ \frac34 \, b \, \mathbf{\hat{y}}- z_{1} \, c \, \mathbf{\hat{z}}& \left(4c\right) & \mbox{Ge} \\ \mathbf{B}_{4} & =&\left(\frac12 + x_{1}\right) \, \mathbf{a}_{1}+ \frac14 \, \mathbf{a}_{2}+ \left(\frac12 - z_{1}\right) \, \mathbf{a}_{3}& =&\left(\frac12 + x_{1}\right) \, a \, \mathbf{\hat{x}}+ \frac14 \, b \, \mathbf{\hat{y}}+ \left(\frac12 - z_{1}\right) \, c \, \mathbf{\hat{z}}& \left(4c\right) & \mbox{Ge} \\ \mathbf{B}_{5} & =&x_{2} \, \mathbf{a}_{1}+ \frac14 \, \mathbf{a}_{2}+ z_{2} \, \mathbf{a}_{3}& =&x_{2} \, a \, \mathbf{\hat{x}}+ \frac14 \, b \, \mathbf{\hat{y}}+ z_{2} \, c \, \mathbf{\hat{z}}& \left(4c\right) & \mbox{S} \\ \mathbf{B}_{6} & =&\left(\frac12 - x_{2}\right) \, \mathbf{a}_{1}+ \frac34 \, \mathbf{a}_{2}+ \left(\frac12 + z_{2}\right) \, \mathbf{a}_{3}& =&\left(\frac12 - x_{2}\right) \, a \, \mathbf{\hat{x}}+ \frac34 \, b \, \mathbf{\hat{y}}+ \left(\frac12 + z_{2}\right) \, c \, \mathbf{\hat{z}}& \left(4c\right) & \mbox{S} \\ \mathbf{B}_{7} & =&- x_{2} \, \mathbf{a}_{1}+ \frac34 \, \mathbf{a}_{2}- z_{2} \, \mathbf{a}_{3}& =&- x_{2} \, a \, \mathbf{\hat{x}}+ \frac34 \, b \, \mathbf{\hat{y}}- z_{2} \, c \, \mathbf{\hat{z}}& \left(4c\right) & \mbox{S} \\ \mathbf{B}_{8} & =&\left(\frac12 + x_{2}\right) \, \mathbf{a}_{1}+ \frac14 \, \mathbf{a}_{2}+ \left(\frac12 - z_{2}\right) \, \mathbf{a}_{3}& =&\left(\frac12 + x_{2}\right) \, a \, \mathbf{\hat{x}}+ \frac14 \, b \, \mathbf{\hat{y}}+ \left(\frac12 - z_{2}\right) \, c \, \mathbf{\hat{z}}& \left(4c\right) & \mbox{S} \\ \end{array} \]References
- W. H. Zachariasen, The Crystal Lattice of Germano Sulphide, GeS, Phys. Rev. 40, 917–922 (1932), doi:10.1103/PhysRev.40.917.
- E. Parthé, L. M. Gelato, B. Chabot, M. Penzo, K. Cenzula, and R. Gladyshevskii, Gmelin Handbook of Inorganic and Organometallic Chemistry: Standardized Data and Crystal Chemical Characterization of Inorganic Structure Types (Springer–Verlag, Berlin and Heidelberg, 1993), 8th edn., doi:10.1007/978-3-662-02909-1_3. Online edition available at DOI. See Table 4.3, pp. 363–371, for a comprehensive compilation of Strukturbericht symbols.
Found in
- R. T. Downs and M. Hall–Wallace, The American Mineralogist Crystal Structure Database, Am. Mineral. 88, 247–250 (2003).