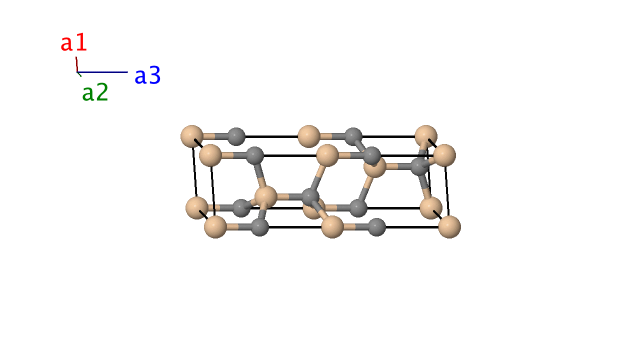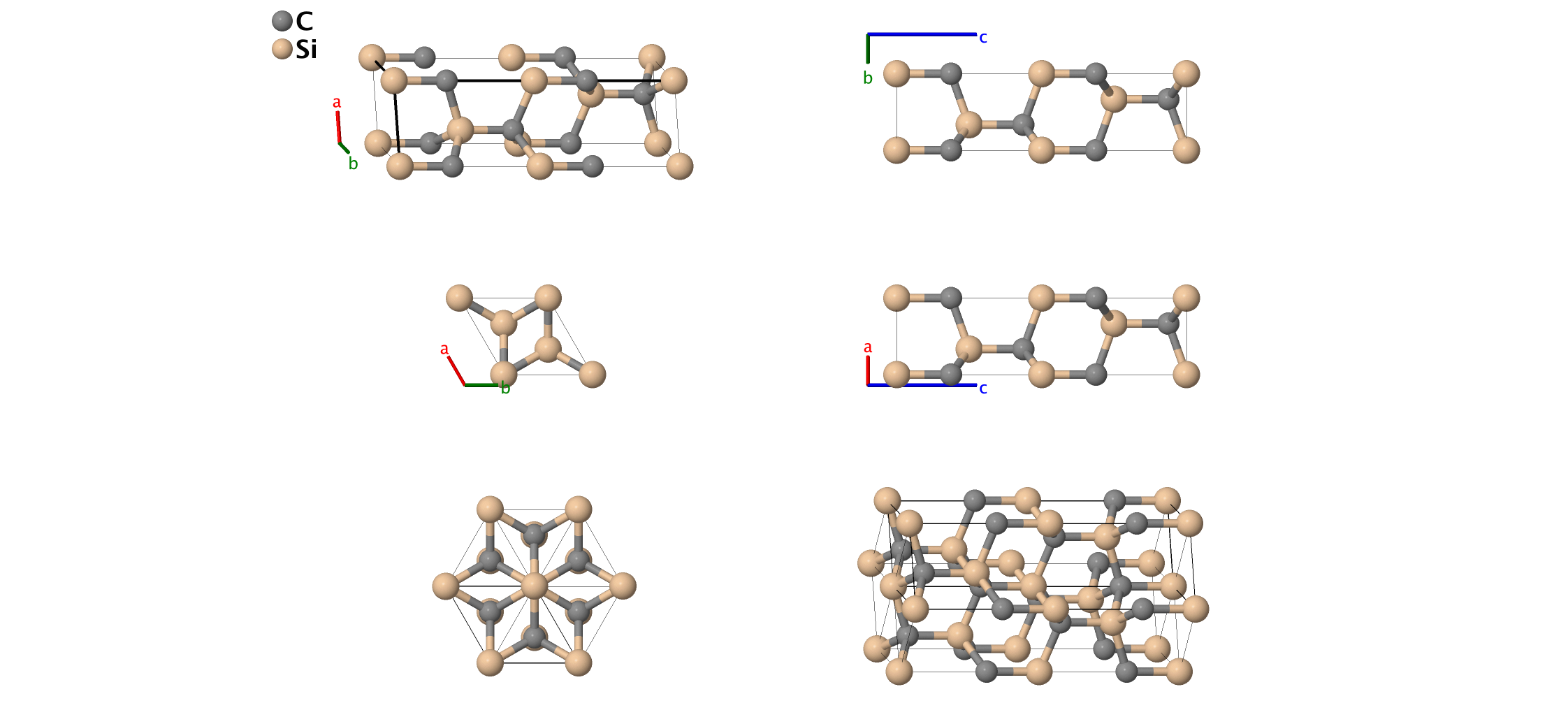
Moissanite–4H SiC (B5) Structure: AB_hP8_186_ab_ab
| Prototype | : | SiC |
| AFLOW prototype label | : | AB_hP8_186_ab_ab |
| Strukturbericht designation | : | $B5$ |
| Pearson symbol | : | hP8 |
| Space group number | : | 186 |
| Space group symbol | : | $\mbox{P6}_{3}\mbox{mc}$ |
| AFLOW prototype command | : | aflow --proto=AB_hP8_186_ab_ab --params=$a,c/a,z_{1},z_{2},z_{3},z_{4}$ |
- This is one possible stacking (ABAC) for tetrahedral structures. Compare this to zincblende (ABCABC), wurtzite (ABABAB), 6H (ABCACB), and 9R (ABCBCACAB). The 4H refers to the fact that there are 4 CSi dimers in a hexagonal unit cell. Zincblende is denoted 3C, and wurtzite is 2H. This structure is related to the $\alpha$–La (A3') structure in the same way that zincblende (B3) is related to the fcc (A1) lattice. Without loss of generality, we can take any of the $z_{i}$ to be zero. In the pictures here we take $z_{1} = 0$.
Hexagonal primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & \frac12 \, a \, \mathbf{\hat{x}} - \frac{\sqrt{3}}{2} \, a \, \mathbf{\hat{y}} \\
\mathbf{a}_2 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2} \, a \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \, \mathbf{\hat{z}}\\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1}& = &z_{1} \, \mathbf{a}_{3}& = &z_{1} \, c \, \mathbf{\hat{z}}& \left(2a\right) & \mbox{C I} \\ \mathbf{B}_{2}& = &\left(\frac12 + z_{1}\right) \, \mathbf{a}_{3}& = &\left(\frac12 + z_{1}\right) \, c \, \mathbf{\hat{z}}& \left(2a\right) & \mbox{C I} \\ \mathbf{B}_{3}& = &z_{2} \, \mathbf{a}_{3}& = &z_{2} \, c \, \mathbf{\hat{z}}& \left(2a\right) & \mbox{Si I} \\ \mathbf{B}_{4}& = &\left(\frac12 + z_{2}\right) \, \mathbf{a}_{3}& = &\left(\frac12 + z_{2}\right) \, c \, \mathbf{\hat{z}}& \left(2a\right) & \mbox{Si I} \\ \mathbf{B}_{5}& = &\frac13 \, \mathbf{a}_{1}+ \frac23 \, \mathbf{a}_{2}+ z_{3} \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\hat{x}}+ \frac1{2\sqrt3} \, a \, \mathbf{\hat{y}}+ z_{3} \, c \, \mathbf{\hat{z}}& \left(2b\right) & \mbox{C II} \\ \mathbf{B}_{6}& = &\frac23 \, \mathbf{a}_{1}+ \frac13 \, \mathbf{a}_{2}+ \left(\frac12 + z_{3}\right) \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\hat{x}}- \frac1{2\sqrt3} \, a \, \mathbf{\hat{y}}+ \left(\frac12 + z_{3}\right) \, c \, \mathbf{\hat{z}}& \left(2b\right) & \mbox{C II} \\ \mathbf{B}_{7}& = &\frac13 \, \mathbf{a}_{1}+ \frac23 \, \mathbf{a}_{2}+ z_{4} \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\hat{x}}+ \frac1{2\sqrt3} \, a \, \mathbf{\hat{y}}+ z_{4} \, c \, \mathbf{\hat{z}}& \left(2b\right) & \mbox{Si II} \\ \mathbf{B}_{8}& = &\frac23 \, \mathbf{a}_{1}+ \frac13 \, \mathbf{a}_{2}+ \left(\frac12 + z_{4}\right) \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\hat{x}}- \frac1{2\sqrt3} \, a \, \mathbf{\hat{y}}+ \left(\frac12 + z_{4}\right) \, c \, \mathbf{\hat{z}}& \left(2b\right) & \mbox{Si II} \\ \end{array} \]References
- A. Bauer, P. Reischauer, J. Kräusslich, N. Schell, W. Matz, and K. Goetz, Structure refinement of the silicon carbide polytypes 4H and 6H: unambiguous determination of the refinement parameters, Acta Crystallogr. Sect. A 57, 60–67 (2001), doi:10.1107/S0108767300012915.