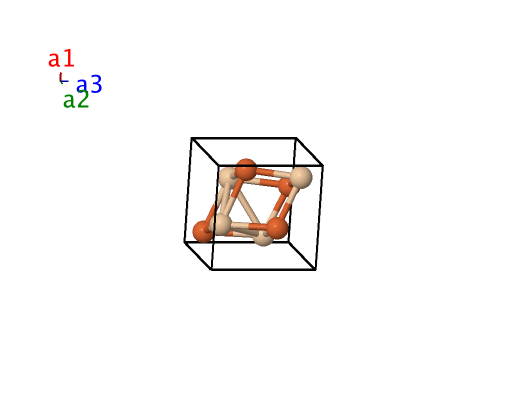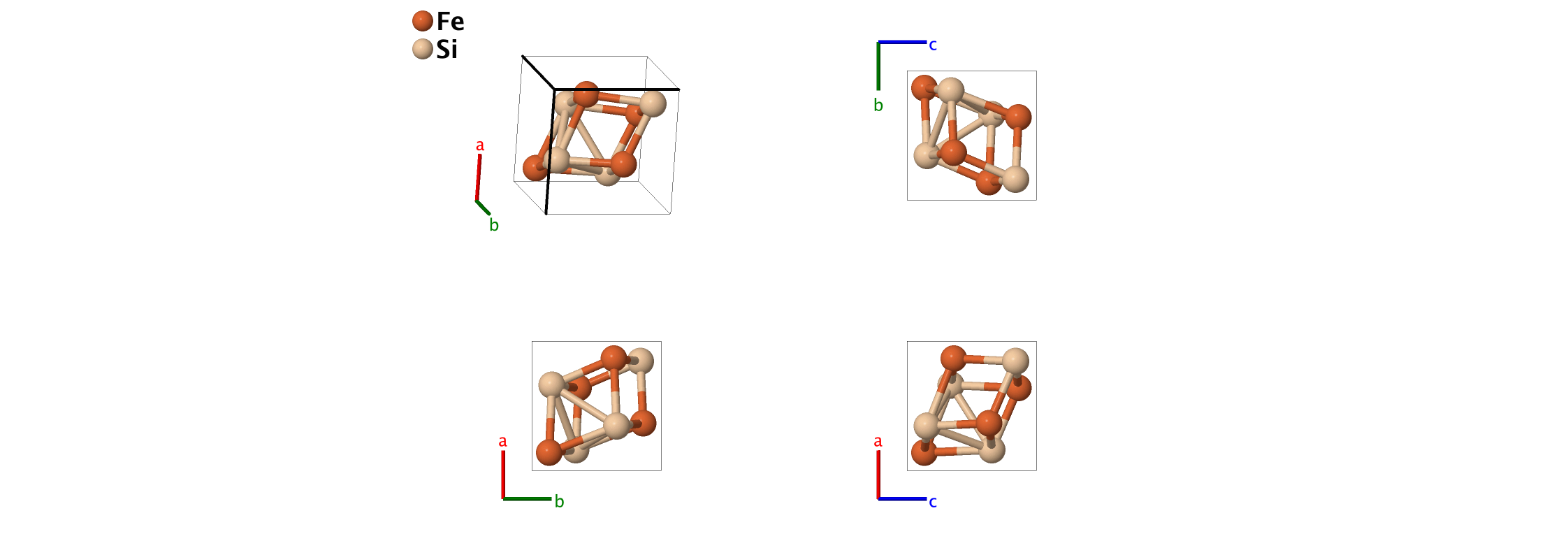
FeSi (B20) Structure: AB_cP8_198_a_a
| Prototype | : | FeSi |
| AFLOW prototype label | : | AB_cP8_198_a_a |
| Strukturbericht designation | : | $B20$ |
| Pearson symbol | : | cP8 |
| Space group number | : | 198 |
| Space group symbol | : | $\mbox{P2}_{1}\mbox{3}$ |
| AFLOW prototype command | : | aflow --proto=AB_cP8_198_a_a --params=$a,x_{1},x_{2}$ |
Other compounds with this structure
- AlPt, AuBe, CoGe, CoSi, FeGe, GaPd, GeMn, GeRh, HfSb, HfSn, RhS, SbZr, SiTc
- When $x_{1} = 0$ and $x_{2} = 1/2$, or $x_{1} = 1/4$ and $x_{2} = 3/4$, this lattice reduces to the rock salt (B1) structure. When $x_{1} = - x_{2} = 1/8 \left(\sqrt5 - 1\right)$ we have an
ideal
structure where every atom is seven-fold coordinated. Note that $\alpha$–CO (AB_cP8_198_a_a, $\alpha$–CO) and FeSi (AB_cP8_198_a_a, FeSi) have the same AFLOW prototype label. They are generated by the same symmetry operations with different sets of parameters (––params) specified in their corresponding CIF files.
Simple Cubic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \\
\mathbf{a}_2 & = & a \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & a \, \mathbf{\hat{z}}
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = &x_{1} \, \mathbf{a}_{1}+ x_{1} \, \mathbf{a}_{2}+ x_{1} \, \mathbf{a}_{3}& = &x_{1} \, a \, \mathbf{\hat{x}}+ x_{1} \, a \, \mathbf{\hat{y}}+ x_{1} \, a \, \mathbf{\hat{z}}& \left(4a\right) & \mbox{Fe} \\ \mathbf{B}_{2} & = &\left(\frac12 - x_{1}\right) \, \mathbf{a}_{1}- x_{1} \, \mathbf{a}_{2}+ \left(\frac12 + x_{1}\right) \, \mathbf{a}_{3}& = &\left(\frac12 - x_{1}\right) \, a \, \mathbf{\hat{x}}- x_{1} \, a \, \mathbf{\hat{y}}+ \left(\frac12 + x_{1}\right) \, a \, \mathbf{\hat{z}}& \left(4a\right) & \mbox{Fe} \\ \mathbf{B}_{3} & = &- x_{1} \, \mathbf{a}_{1}+ \left(\frac12 + x_{1}\right) \, \mathbf{a}_{2}+ \left(\frac12 - x_{1}\right) \, \mathbf{a}_{3}& = &- x_{1} \, a \, \mathbf{\hat{x}}+ \left(\frac12 + x_{1}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac12 - x_{1}\right) \, a \, \mathbf{\hat{z}}& \left(4a\right) & \mbox{Fe} \\ \mathbf{B}_{4} & = &+ \left(\frac12 + x_{1}\right) \, \mathbf{a}_{1}+ \left(\frac12 - x_{1}\right) \, \mathbf{a}_{2}- x_{1} \, \mathbf{a}_{3}& = &+ \left(\frac12 + x_{1}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - x_{1}\right) \, a \, \mathbf{\hat{y}}- x_{1} \, a \, \mathbf{\hat{z}}& \left(4a\right) & \mbox{Fe} \\ \mathbf{B}_{5} & = &x_{2} \, \mathbf{a}_{1}+ x_{2} \, \mathbf{a}_{2}+ x_{2} \, \mathbf{a}_{3}& = &x_{2} \, a \, \mathbf{\hat{x}}+ x_{2} \, a \, \mathbf{\hat{y}}+ x_{2} \, a \, \mathbf{\hat{z}}& \left(4a\right) & \mbox{Si} \\ \mathbf{B}_{6} & = &\left(\frac12 - x_{2}\right) \, \mathbf{a}_{1}- x_{2} \, \mathbf{a}_{2}+ \left(\frac12 + x_{2}\right) \, \mathbf{a}_{3}& = &\left(\frac12 - x_{2}\right) \, a \, \mathbf{\hat{x}}- x_{2} \, a \, \mathbf{\hat{y}}+ \left(\frac12 + x_{2}\right) \, a \, \mathbf{\hat{z}}& \left(4a\right) & \mbox{Si} \\ \mathbf{B}_{7} & = &- x_{2} \, \mathbf{a}_{1}+ \left(\frac12 + x_{2}\right) \, \mathbf{a}_{2}+ \left(\frac12 - x_{2}\right) \, \mathbf{a}_{3}& = &- x_{2} \, a \, \mathbf{\hat{x}}+ \left(\frac12 + x_{2}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac12 - x_{2}\right) \, a \, \mathbf{\hat{z}}& \left(4a\right) & \mbox{Si} \\ \mathbf{B}_{8} & = &+ \left(\frac12 + x_{2}\right) \, \mathbf{a}_{1}+ \left(\frac12 - x_{2}\right) \, \mathbf{a}_{2}- x_{2} \, \mathbf{a}_{3}& = &+ \left(\frac12 + x_{2}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - x_{2}\right) \, a \, \mathbf{\hat{y}}- x_{2} \, a \, \mathbf{\hat{z}}& \left(4a\right) & \mbox{Si} \\ \end{array} \]References
- L. Vovcadlo, K. S. Knight, G. D. Price, and I. G. Wood, Thermal expansion and crystal structure of FeSi between 4 and 1173 K determined by time–of–flight neutron powder diffraction, Phys. Chem. Miner. 29, 132–139 (2002), doi:10.1007/s002690100202.