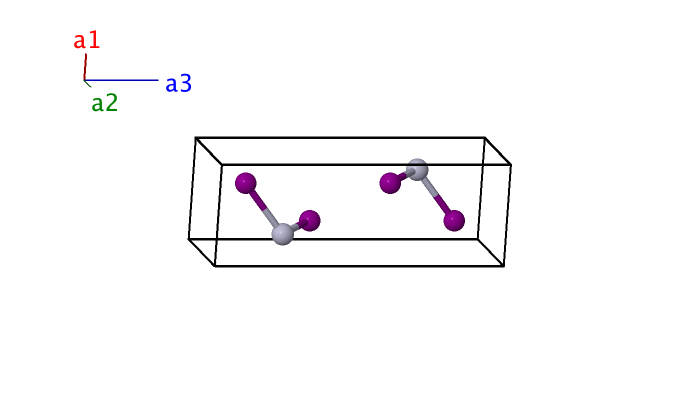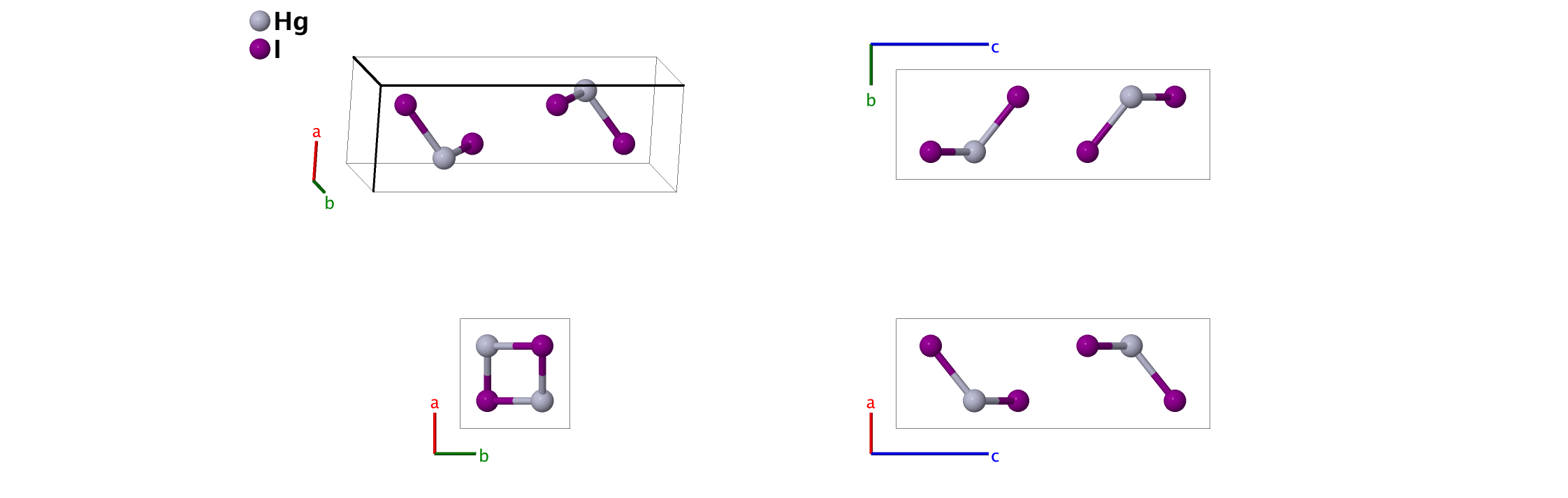
HgI2 ($C13$) Structure: AB2_tP6_137_a_d
| Prototype | : | HgI |
| AFLOW prototype label | : | AB2_tP6_137_a_d |
| Strukturbericht designation | : | $C13$ |
| Pearson symbol | : | tP6 |
| Space group number | : | 137 |
| Space group symbol | : | $P4_{2}/nmc$ |
| AFLOW prototype command | : | aflow --proto=AB2_tP6_137_a_d --params=$a,c/a,z_{2}$ |
- The CIF and POSCAR files contain the data at room temperature, 293 K. ZrO2 (A2B_tP6_137_d_a) and HgI2 (AB2_tP6_137_a_d) have similar AFLOW prototype labels (i.e., same symmetry and set of Wyckoff positions with different stoichiometry labels due to alphabetic ordering of atomic species). They are generated by the same symmetry operations with different sets of parameters (––params) specified in their corresponding CIF files.
Simple Tetragonal primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \\
\mathbf{a}_2 & = & a \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \, \mathbf{\hat{z}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = & \frac{3}{4} \, \mathbf{a}_{1} + \frac{1}{4} \, \mathbf{a}_{2} + \frac{3}{4} \, \mathbf{a}_{3} & = & \frac{3}{4}a \, \mathbf{\hat{x}} + \frac{1}{4}a \, \mathbf{\hat{y}} + \frac{3}{4}c \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{Hg} \\ \mathbf{B}_{2} & = & \frac{1}{4} \, \mathbf{a}_{1} + \frac{3}{4} \, \mathbf{a}_{2} + \frac{1}{4} \, \mathbf{a}_{3} & = & \frac{1}{4}a \, \mathbf{\hat{x}} + \frac{3}{4}a \, \mathbf{\hat{y}} + \frac{1}{4}c \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{Hg} \\ \mathbf{B}_{3} & = & \frac{1}{4} \, \mathbf{a}_{1} + \frac{1}{4} \, \mathbf{a}_{2} + z_{2} \, \mathbf{a}_{3} & = & \frac{1}{4}a \, \mathbf{\hat{x}} + \frac{1}{4}a \, \mathbf{\hat{y}} + z_{2}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{I} \\ \mathbf{B}_{4} & = & \frac{1}{4} \, \mathbf{a}_{1} + \frac{1}{4} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{2}\right) \, \mathbf{a}_{3} & = & \frac{1}{4}a \, \mathbf{\hat{x}} + \frac{1}{4}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{2}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{I} \\ \mathbf{B}_{5} & = & \frac{3}{4} \, \mathbf{a}_{1} + \frac{3}{4} \, \mathbf{a}_{2}-z_{2} \, \mathbf{a}_{3} & = & \frac{3}{4}a \, \mathbf{\hat{x}} + \frac{3}{4}a \, \mathbf{\hat{y}}-z_{2}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{I} \\ \mathbf{B}_{6} & = & \frac{3}{4} \, \mathbf{a}_{1} + \frac{3}{4} \, \mathbf{a}_{2} + \left(\frac{1}{2} - z_{2}\right) \, \mathbf{a}_{3} & = & \frac{3}{4}a \, \mathbf{\hat{x}} + \frac{3}{4}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} - z_{2}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{I} \\ \end{array} \]References
- D. Schwarzenbach, H. Birkedal, M. Hostettler, and P. Fischer, Neutron diffraction investigation of the temperature dependence of crystal structure and thermal motions of red HgI2, Acta Crystallogr. Sect. B Struct. Sci. 63, 828–835 (2007), doi:10.1107/S0108768107043327.
Found in
- R. T. Downs and M. Hall–Wallace, The American Mineralogist Crystal Structure Database, Am. Mineral. 88, 247–250 (2003).