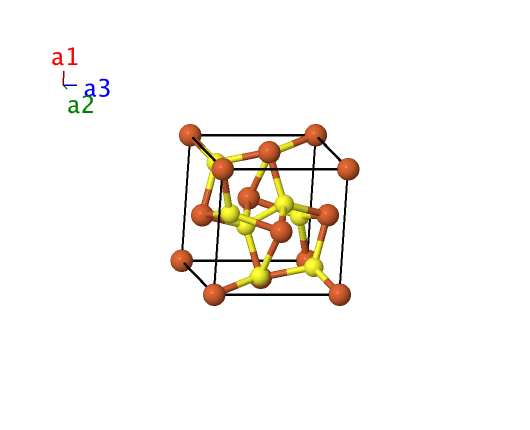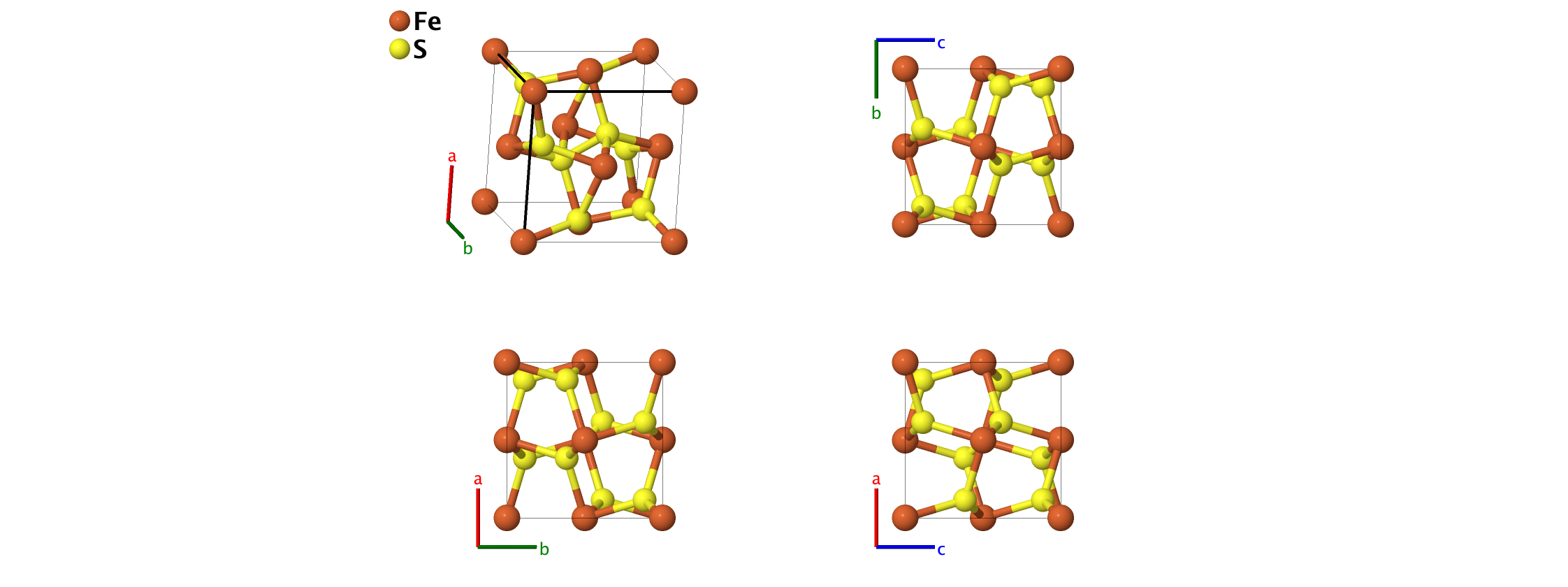
Pyrite (FeS2, C2) Structure: AB2_cP12_205_a_c
| Prototype | : | FeS2 |
| AFLOW prototype label | : | AB2_cP12_205_a_c |
| Strukturbericht designation | : | $C2$ |
| Pearson symbol | : | cP12 |
| Space group number | : | 205 |
| Space group symbol | : | $\mbox{Pa}\bar{3}$ |
| AFLOW prototype command | : | aflow --proto=AB2_cP12_205_a_c --params=$a,x_{2}$ |
Other compounds with this structure
- AuSb2, CaC2, CoS2, MnS2, NiS2, NiSe2, OsS2, OsTe2, PdAs2, PtAs2, PtBi2, RhSe2, RuS2
- (Bayliss, 1997) gives crystalline data for
weakly anisotropic pyrite
which we have tabulated as P1 FeS2. He also gives crystallographic data for the cubic pyrite structure, which we report here. Also see the C18 (marcasite) FeS2 structure.
Simple Cubic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & a \, \mathbf{\mathbf{\hat{x}}} \\
\mathbf{a}_2 & = & a \, \mathbf{\mathbf{\hat{y}}} \\
\mathbf{a}_3 & = & a \, \mathbf{\mathbf{\hat{z}}}
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = &0 \, \mathbf{a}_{1} + 0 \, \mathbf{a}_{2} + 0 \, \mathbf{a}_{3} & = &0 \mathbf{\mathbf{\hat{x}}} + 0 \mathbf{\mathbf{\hat{y}}} + 0 \mathbf{\mathbf{\hat{z}}} & \left(4a\right) & \mbox{Fe} \\ \mathbf{B}_{2} & = &\frac12 \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\mathbf{\hat{x}}}+ \frac12 \, a \, \mathbf{\mathbf{\hat{z}}}& \left(4a\right) & \mbox{Fe} \\ \mathbf{B}_{3} & = &\frac12 \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\mathbf{\hat{y}}}+ \frac12 \, a \, \mathbf{\mathbf{\hat{z}}}& \left(4a\right) & \mbox{Fe} \\ \mathbf{B}_{4} & = &\frac12 \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{2}& = &\frac12 \, a \, \mathbf{\mathbf{\hat{x}}}+ \frac12 \, a \, \mathbf{\mathbf{\hat{y}}}& \left(4a\right) & \mbox{Fe} \\ \mathbf{B}_{5} & = &x_{2} \, \mathbf{a}_{1}+ x_{2} \, \mathbf{a}_{2}+ x_{2} \, \mathbf{a}_{3}& = &x_{2} \, a \, \mathbf{\mathbf{\hat{x}}}+ x_{2} \, a \, \mathbf{\mathbf{\hat{y}}}+ x_{2} \, a \, \mathbf{\mathbf{\hat{z}}}& \left(8c\right) & \mbox{S} \\ \mathbf{B}_{6} & = &\left(\frac12 - x_{2}\right) \, \mathbf{a}_{1}- x_{2} \, \mathbf{a}_{2}+ \left(\frac12 + x_{2}\right) \, \mathbf{a}_{3}& = &\left(\frac12 - x_{2}\right) \, a \, \mathbf{\mathbf{\hat{x}}}- x_{2} \, a \, \mathbf{\mathbf{\hat{y}}}+ \left(\frac12 + x_{2}\right) \, a \, \mathbf{\mathbf{\hat{z}}}& \left(8c\right) & \mbox{S} \\ \mathbf{B}_{7} & = &- x_{2} \, \mathbf{a}_{1}+ \left(\frac12 + x_{2}\right) \, \mathbf{a}_{2}+ \left(\frac12 - x_{2}\right) \, \mathbf{a}_{3}& = &- x_{2} \, a \, \mathbf{\mathbf{\hat{x}}}+ \left(\frac12 + x_{2}\right) \, a \, \mathbf{\mathbf{\hat{y}}}+ \left(\frac12 - x_{2}\right) \, a \, \mathbf{\mathbf{\hat{z}}}& \left(8c\right) & \mbox{S} \\ \mathbf{B}_{8} & = &\left(\frac12 + x_{2}\right) \, \mathbf{a}_{1}+ \left(\frac12 - x_{2}\right) \, \mathbf{a}_{2}- x_{2} \, \mathbf{a}_{3}& = &\left(\frac12 + x_{2}\right) \, a \, \mathbf{\mathbf{\hat{x}}}+ \left(\frac12 - x_{2}\right) \, a \, \mathbf{\mathbf{\hat{y}}}- x_{2} \, a \, \mathbf{\mathbf{\hat{z}}}& \left(8c\right) & \mbox{S} \\ \mathbf{B}_{9} & = &- x_{2} \, \mathbf{a}_{1}- x_{2} \, \mathbf{a}_{2}- x_{2} \, \mathbf{a}_{3}& = &- x_{2} \, a \, \mathbf{\mathbf{\hat{x}}}- x_{2} \, a \, \mathbf{\mathbf{\hat{y}}}- x_{2} \, a \, \mathbf{\mathbf{\hat{z}}}& \left(8c\right) & \mbox{S} \\ \mathbf{B}_{10} & = &\left(\frac12 + x_{2}\right) \, \mathbf{a}_{1}+ x_{2} \, \mathbf{a}_{2}+ \left(\frac12 - x_{2}\right) \, \mathbf{a}_{3}& = &\left(\frac12 + x_{2}\right) \, a \, \mathbf{\mathbf{\hat{x}}}+ x_{2} \, a \, \mathbf{\mathbf{\hat{y}}}+ \left(\frac12 - x_{2}\right) \, a \, \mathbf{\mathbf{\hat{z}}}& \left(8c\right) & \mbox{S} \\ \mathbf{B}_{11} & = &x_{2} \, \mathbf{a}_{1}+ \left(\frac12 - x_{2}\right) \, \mathbf{a}_{2}+ \left(\frac12 + x_{2}\right) \, \mathbf{a}_{3}& = &x_{2} \, a \, \mathbf{\mathbf{\hat{x}}}+ \left(\frac12 - x_{2}\right) \, a \, \mathbf{\mathbf{\hat{y}}}+ \left(\frac12 + x_{2}\right) \, a \, \mathbf{\mathbf{\hat{z}}}& \left(8c\right) & \mbox{S} \\ \mathbf{B}_{12} & = &\left(\frac12 - x_{2}\right) \, \mathbf{a}_{1}+ \left(\frac12 + x_{2}\right) \, \mathbf{a}_{2}+ x_{2} \, \mathbf{a}_{3}& = &\left(\frac12 - x_{2}\right) \, a \, \mathbf{\mathbf{\hat{x}}}+ \left(\frac12 + x_{2}\right) \, a \, \mathbf{\mathbf{\hat{y}}}+ x_{2} \, a \, \mathbf{\mathbf{\hat{z}}}& \left(8c\right) & \mbox{S} \\ \end{array} \]References
- P. Bayliss, Crystal structure refinement of a weakly anisotropic pyrite, Am. Mineral. 62, 1168–1172 (1977).
Found in
- R. T. Downs and M. Hall–Wallace, The American Mineralogist Crystal Structure Database, Am. Mineral. 88, 247–250 (2003).