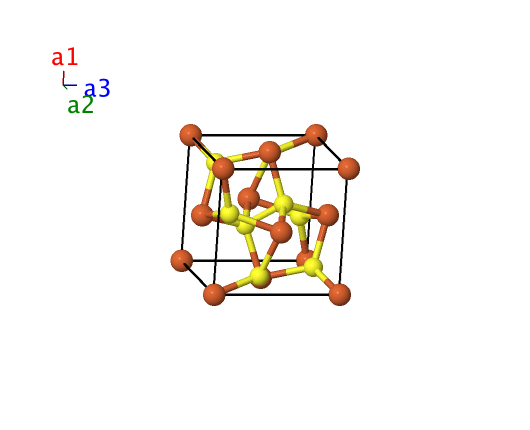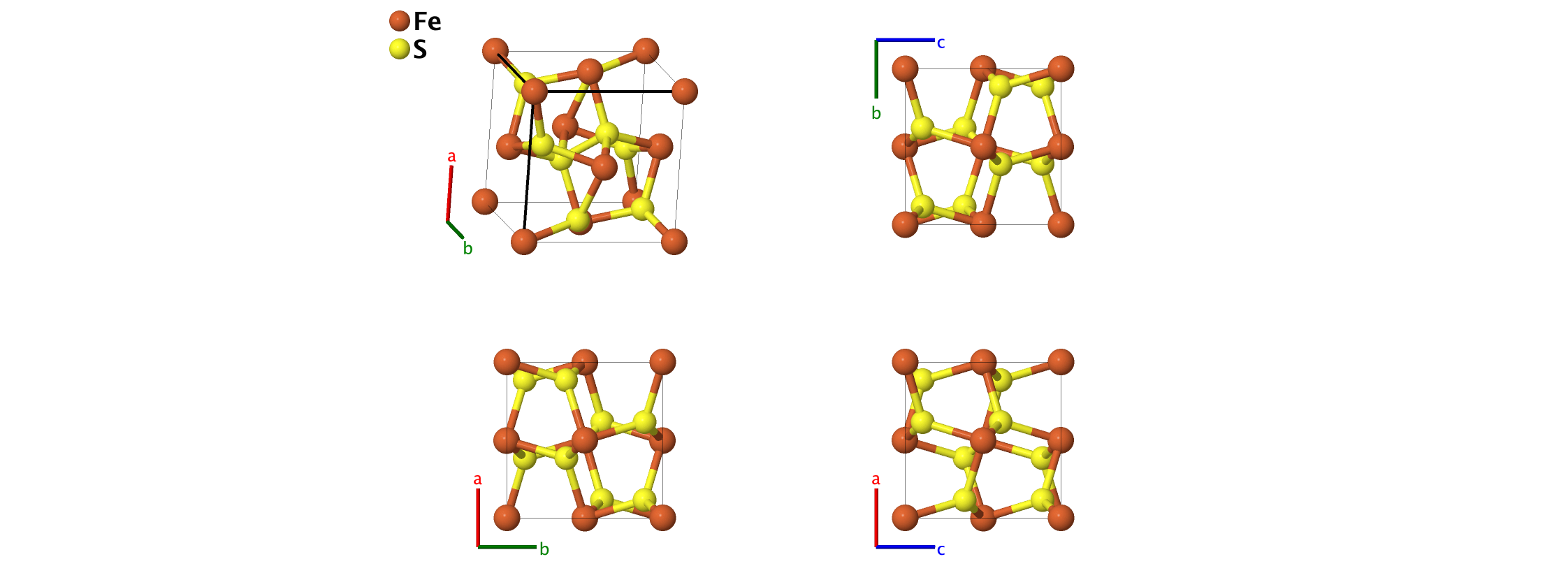
FeS2 (P1) Structure: AB2_aP12_1_4a_8a
| Prototype | : | FeS2 |
| AFLOW prototype label | : | AB2_aP12_1_4a_8a |
| Strukturbericht designation | : | None |
| Pearson symbol | : | aP12 |
| Space group number | : | 1 |
| Space group symbol | : | $\mbox{P1}$ |
| AFLOW prototype command | : | aflow --proto=AB2_aP12_1_4a_8a --params=$a,b/a,c/a,\alpha,\beta,\gamma,x_{1},y_{1},z_{1},x_{2},y_{2},z_{2},x_{3},y_{3},z_{3},x_{4},y_{4},z_{4},x_{5},y_{5},z_{5},x_{6}, \\y_{6},z_{6},x_{7},y_{7},z_{7},x_{8},y_{8},z_{8},x_{9},y_{9},z_{9},x_{10},y_{10},z_{10},x_{11},y_{11},z_{11},x_{12},y_{12},z_{12}$ |
- This structure is just a slightly distorted version of pyrite (C2), with no rotational symmetry whatsoever.
Triclinic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & a \mathbf{\hat{x}} \\
\mathbf{a}_2 & = & b \cos\gamma \, \mathbf{\hat{x}} + b \sin\gamma \,\mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c_x \mathbf{\hat{x}}
+ c_y \, \mathbf{\hat{y}}
+ c_z \, \mathbf{\hat{z}}
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & =& x_{1} \, \mathbf{a}_{1} + y_{1} \, \mathbf{a}_{2} + z_{1} \, \mathbf{a}_{3}& =& \left(x_{1} \, a + y_{1} \, b \, \cos\gamma \, + z_{1} \, c_x\right)\, \mathbf{\hat{x}}+ \left(y_{1} \, b \, \sin\gamma + z_{1} \, c_y\right) \, \mathbf{\hat{y}}+ z_{1} \, c_z \, \mathbf{\hat{z}}& \left(1a\right) & \mbox{Fe I} \\ \mathbf{B}_{2} & =& x_{2} \, \mathbf{a}_{1} + y_{2} \, \mathbf{a}_{2} + z_{2} \, \mathbf{a}_{3}& =& \left(x_{2} \, a + y_{2} \, b \, \cos\gamma \, + z_{2} \, c_x\right)\, \mathbf{\hat{x}}+ \left(y_{2} \, b \, \sin\gamma + z_{2} \, c_y\right) \, \mathbf{\hat{y}}+ z_{2} \, c_z \, \mathbf{\hat{z}}& \left(1a\right) & \mbox{Fe II} \\ \mathbf{B}_{3} & =& x_{3} \, \mathbf{a}_{1} + y_{3} \, \mathbf{a}_{2} + z_{3} \, \mathbf{a}_{3}& =& \left(x_{3} \, a + y_{3} \, b \, \cos\gamma \, + z_{3} \, c_x\right)\, \mathbf{\hat{x}}+ \left(y_{3} \, b \, \sin\gamma + z_{3} \, c_y\right) \, \mathbf{\hat{y}}+ z_{3} \, c_z \, \mathbf{\hat{z}}& \left(1a\right) & \mbox{Fe III} \\ \mathbf{B}_{4} & =& x_{4} \, \mathbf{a}_{1} + y_{4} \, \mathbf{a}_{2} + z_{4} \, \mathbf{a}_{3}& =& \left(x_{4} \, a + y_{4} \, b \, \cos\gamma \, + z_{4} \, c_x\right)\, \mathbf{\hat{x}}+ \left(y_{4} \, b \, \sin\gamma + z_{4} \, c_y\right) \, \mathbf{\hat{y}}+ z_{4} \, c_z \, \mathbf{\hat{z}}& \left(1a\right) & \mbox{Fe IV} \\ \mathbf{B}_{5} & =& x_{5} \, \mathbf{a}_{1} + y_{5} \, \mathbf{a}_{2} + z_{5} \, \mathbf{a}_{3}& =& \left(x_{5} \, a + y_{5} \, b \, \cos\gamma \, + z_{5} \, c_x\right)\, \mathbf{\hat{x}}+ \left(y_{5} \, b \, \sin\gamma + z_{5} \, c_y\right) \, \mathbf{\hat{y}}+ z_{5} \, c_z \, \mathbf{\hat{z}}& \left(1a\right) & \mbox{S I} \\ \mathbf{B}_{6} & =& x_{6} \, \mathbf{a}_{1} + y_{6} \, \mathbf{a}_{2} + z_{6} \, \mathbf{a}_{3}& =& \left(x_{6} \, a + y_{6} \, b \, \cos\gamma \, + z_{6} \, c_x\right)\, \mathbf{\hat{x}}+ \left(y_{6} \, b \, \sin\gamma + z_{6} \, c_y\right) \, \mathbf{\hat{y}}+ z_{6} \, c_z \, \mathbf{\hat{z}}& \left(1a\right) & \mbox{S II} \\ \mathbf{B}_{7} & =& x_{7} \, \mathbf{a}_{1} + y_{7} \, \mathbf{a}_{2} + z_{7} \, \mathbf{a}_{3}& =& \left(x_{7} \, a + y_{7} \, b \, \cos\gamma \, + z_{7} \, c_x\right)\, \mathbf{\hat{x}}+ \left(y_{7} \, b \, \sin\gamma + z_{7} \, c_y\right) \, \mathbf{\hat{y}}+ z_{7} \, c_z \, \mathbf{\hat{z}}& \left(1a\right) & \mbox{S III} \\ \mathbf{B}_{8} & =& x_{8} \, \mathbf{a}_{1} + y_{8} \, \mathbf{a}_{2} + z_{8} \, \mathbf{a}_{3}& =& \left(x_{8} \, a + y_{8} \, b \, \cos\gamma \, + z_{8} \, c_x\right)\, \mathbf{\hat{x}}+ \left(y_{8} \, b \, \sin\gamma + z_{8} \, c_y\right) \, \mathbf{\hat{y}}+ z_{8} \, c_z \, \mathbf{\hat{z}}& \left(1a\right) & \mbox{S IV} \\ \mathbf{B}_{9} & =& x_{9} \, \mathbf{a}_{1} + y_{9} \, \mathbf{a}_{2} + z_{9} \, \mathbf{a}_{3}& =& \left(x_{9} \, a + y_{9} \, b \, \cos\gamma \, + z_{9} \, c_x\right)\, \mathbf{\hat{x}}+ \left(y_{9} \, b \, \sin\gamma + z_{9} \, c_y\right) \, \mathbf{\hat{y}}+ z_{9} \, c_z \, \mathbf{\hat{z}}& \left(1a\right) & \mbox{S V} \\ \mathbf{B}_{10} & =& x_{10} \, \mathbf{a}_{1} + y_{10} \, \mathbf{a}_{2} + z_{10} \, \mathbf{a}_{3}& =& \left(x_{10} \, a + y_{10} \, b \, \cos\gamma \, + z_{10} \, c_x\right)\, \mathbf{\hat{x}}+ \left(y_{10} \, b \, \sin\gamma + z_{10} \, c_y\right) \, \mathbf{\hat{y}}+ z_{10} \, c_z \, \mathbf{\hat{z}}& \left(1a\right) & \mbox{S VI} \\ \mathbf{B}_{11} & =& x_{11} \, \mathbf{a}_{1} + y_{11} \, \mathbf{a}_{2} + z_{11} \, \mathbf{a}_{3}& =& \left(x_{11} \, a + y_{11} \, b \, \cos\gamma \, + z_{11} \, c_x\right)\, \mathbf{\hat{x}}+ \left(y_{11} \, b \, \sin\gamma + z_{11} \, c_y\right) \, \mathbf{\hat{y}}+ z_{11} \, c_z \, \mathbf{\hat{z}}& \left(1a\right) & \mbox{S VII} \\ \mathbf{B}_{12} & =& x_{12} \, \mathbf{a}_{1} + y_{12} \, \mathbf{a}_{2} + z_{12} \, \mathbf{a}_{3}& =& \left(x_{12} \, a + y_{12} \, b \, \cos\gamma \, + z_{12} \, c_x\right)\, \mathbf{\hat{x}}+ \left(y_{12} \, b \, \sin\gamma + z_{12} \, c_y\right) \, \mathbf{\hat{y}}+ z_{12} \, c_z \, \mathbf{\hat{z}}& \left(1a\right) & \mbox{S VIII} \\ \end{array} \]References
- P. Bayliss, Crystal structure refinement of a weakly anisotropic pyrite, Am. Mineral. 62, 1168–1172 (1977).