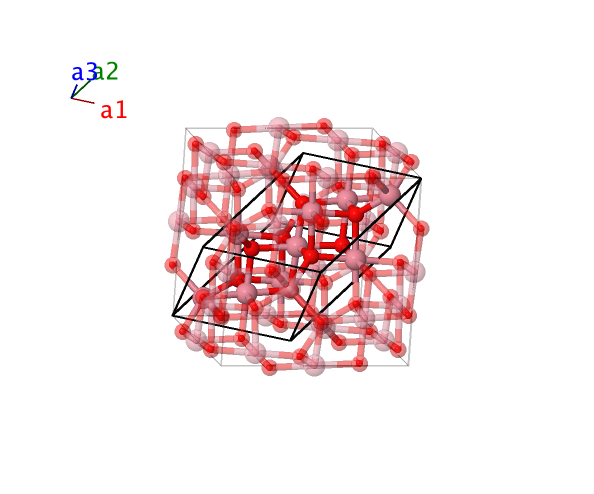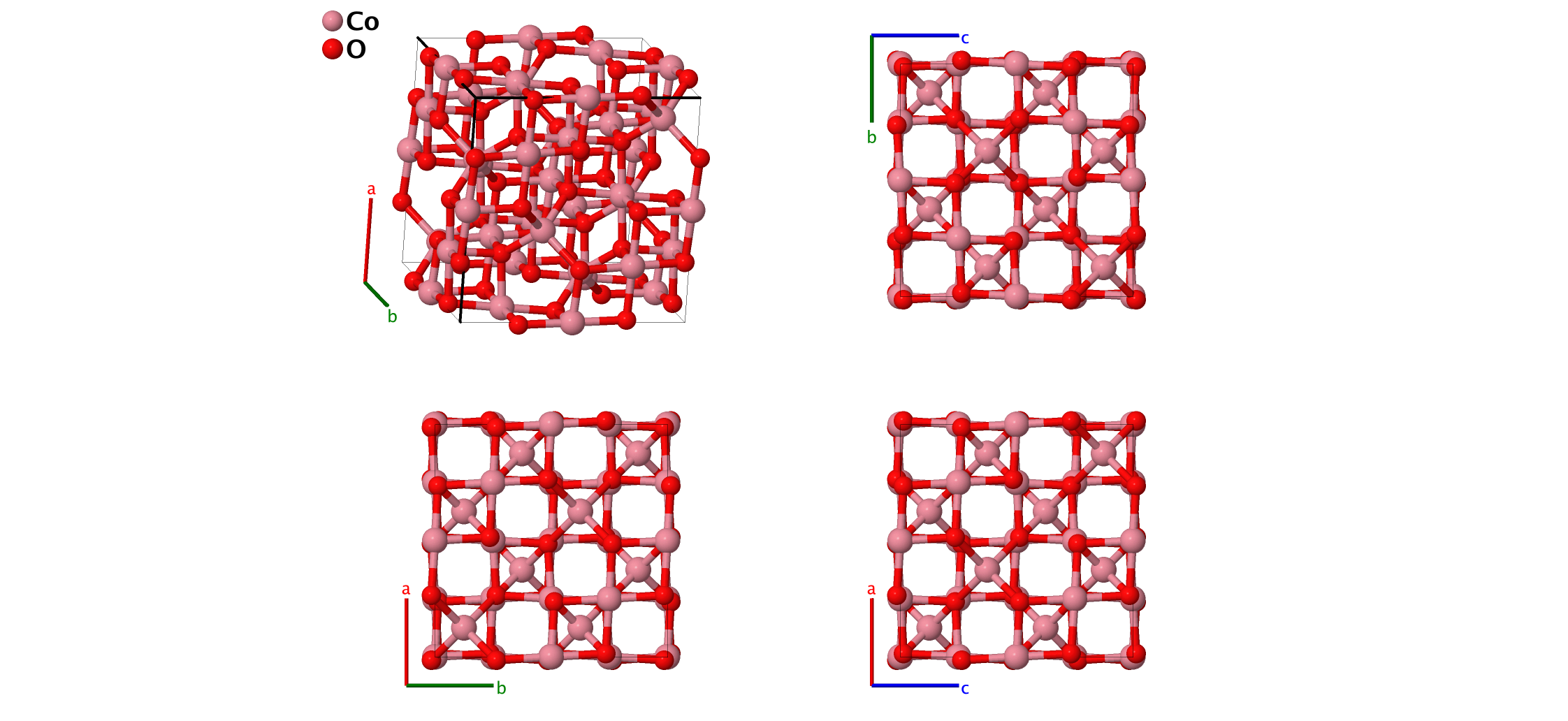
Spinel (Co3O4, $D7_{2}$) Structure: A3B4_cF56_227_ad_e
| Prototype | : | Co3O4 |
| AFLOW prototype label | : | A3B4_cF56_227_ad_e |
| Strukturbericht designation | : | $D7_{2}$ |
| Pearson symbol | : | cF56 |
| Space group number | : | 227 |
| Space group symbol | : | $Fd\bar{3}m$ |
| AFLOW prototype command | : | aflow --proto=A3B4_cF56_227_ad_e --params=$a,x_{3}$ |
Other compounds with this structure:
- NiCo2O4, Co3S4, NiCo2S4, FeNi2S4
- The $D7_{2}$ and $H1_{1}$ Spinel structures are for all intents and purposes identical. We could use $D7_{3}$ for the binary spinels and $H1_{1}$ for the ternaries, but historically this has not been the case. We dual-list this structure only to keep the historical record intact. (Hahn, 1955) has an extensive list of ternary spinels and inverse spinels.
Face-centered Cubic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & \frac12 \, a \, \mathbf{\hat{y}} + \frac12 \, a \, \mathbf{\hat{z}} \\
\mathbf{a}_2 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, a \, \mathbf{\hat{z}} \\
\mathbf{a}_3 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, a \, \mathbf{\hat{y}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = & \frac{1}{8} \, \mathbf{a}_{1} + \frac{1}{8} \, \mathbf{a}_{2} + \frac{1}{8} \, \mathbf{a}_{3} & = & \frac{1}{8}a \, \mathbf{\hat{x}} + \frac{1}{8}a \, \mathbf{\hat{y}} + \frac{1}{8}a \, \mathbf{\hat{z}} & \left(8a\right) & \mbox{Co I} \\ \mathbf{B}_{2} & = & \frac{7}{8} \, \mathbf{a}_{1} + \frac{7}{8} \, \mathbf{a}_{2} + \frac{7}{8} \, \mathbf{a}_{3} & = & \frac{7}{8}a \, \mathbf{\hat{x}} + \frac{7}{8}a \, \mathbf{\hat{y}} + \frac{7}{8}a \, \mathbf{\hat{z}} & \left(8a\right) & \mbox{Co I} \\ \mathbf{B}_{3} & = & \frac{1}{2} \, \mathbf{a}_{1} + \frac{1}{2} \, \mathbf{a}_{2} + \frac{1}{2} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{x}} + \frac{1}{2}a \, \mathbf{\hat{y}} + \frac{1}{2}a \, \mathbf{\hat{z}} & \left(16d\right) & \mbox{Co II} \\ \mathbf{B}_{4} & = & \frac{1}{2} \, \mathbf{a}_{1} + \frac{1}{2} \, \mathbf{a}_{2} & = & \frac{1}{4}a \, \mathbf{\hat{x}} + \frac{1}{4}a \, \mathbf{\hat{y}} + \frac{1}{2}a \, \mathbf{\hat{z}} & \left(16d\right) & \mbox{Co II} \\ \mathbf{B}_{5} & = & \frac{1}{2} \, \mathbf{a}_{1} + \frac{1}{2} \, \mathbf{a}_{3} & = & \frac{1}{4}a \, \mathbf{\hat{x}} + \frac{1}{2}a \, \mathbf{\hat{y}} + \frac{1}{4}a \, \mathbf{\hat{z}} & \left(16d\right) & \mbox{Co II} \\ \mathbf{B}_{6} & = & \frac{1}{2} \, \mathbf{a}_{2} + \frac{1}{2} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{x}} + \frac{1}{4}a \, \mathbf{\hat{y}} + \frac{1}{4}a \, \mathbf{\hat{z}} & \left(16d\right) & \mbox{Co II} \\ \mathbf{B}_{7} & = & x_{3} \, \mathbf{a}_{1} + x_{3} \, \mathbf{a}_{2} + x_{3} \, \mathbf{a}_{3} & = & x_{3}a \, \mathbf{\hat{x}} + x_{3}a \, \mathbf{\hat{y}} + x_{3}a \, \mathbf{\hat{z}} & \left(32e\right) & \mbox{O} \\ \mathbf{B}_{8} & = & x_{3} \, \mathbf{a}_{1} + x_{3} \, \mathbf{a}_{2} + \left(\frac{1}{2} - 3x_{3}\right) \, \mathbf{a}_{3} & = & \left(\frac{1}{4} - x_{3}\right)a \, \mathbf{\hat{x}} + \left(\frac{1}{4} - x_{3}\right)a \, \mathbf{\hat{y}} + x_{3}a \, \mathbf{\hat{z}} & \left(32e\right) & \mbox{O} \\ \mathbf{B}_{9} & = & x_{3} \, \mathbf{a}_{1} + \left(\frac{1}{2} - 3x_{3}\right) \, \mathbf{a}_{2} + x_{3} \, \mathbf{a}_{3} & = & \left(\frac{1}{4} - x_{3}\right)a \, \mathbf{\hat{x}} + x_{3}a \, \mathbf{\hat{y}} + \left(\frac{1}{4} - x_{3}\right)a \, \mathbf{\hat{z}} & \left(32e\right) & \mbox{O} \\ \mathbf{B}_{10} & = & \left(\frac{1}{2} - 3x_{3}\right) \, \mathbf{a}_{1} + x_{3} \, \mathbf{a}_{2} + x_{3} \, \mathbf{a}_{3} & = & x_{3}a \, \mathbf{\hat{x}} + \left(\frac{1}{4} - x_{3}\right)a \, \mathbf{\hat{y}} + \left(\frac{1}{4} - x_{3}\right)a \, \mathbf{\hat{z}} & \left(32e\right) & \mbox{O} \\ \mathbf{B}_{11} & = & -x_{3} \, \mathbf{a}_{1}-x_{3} \, \mathbf{a}_{2} + \left(\frac{1}{2} +3x_{3}\right) \, \mathbf{a}_{3} & = & \left(\frac{1}{4} +x_{3}\right)a \, \mathbf{\hat{x}} + \left(\frac{1}{4} +x_{3}\right)a \, \mathbf{\hat{y}}-x_{3}a \, \mathbf{\hat{z}} & \left(32e\right) & \mbox{O} \\ \mathbf{B}_{12} & = & -x_{3} \, \mathbf{a}_{1}-x_{3} \, \mathbf{a}_{2}-x_{3} \, \mathbf{a}_{3} & = & -x_{3}a \, \mathbf{\hat{x}}-x_{3}a \, \mathbf{\hat{y}}-x_{3}a \, \mathbf{\hat{z}} & \left(32e\right) & \mbox{O} \\ \mathbf{B}_{13} & = & -x_{3} \, \mathbf{a}_{1} + \left(\frac{1}{2} +3x_{3}\right) \, \mathbf{a}_{2}-x_{3} \, \mathbf{a}_{3} & = & \left(\frac{1}{4} +x_{3}\right)a \, \mathbf{\hat{x}}-x_{3}a \, \mathbf{\hat{y}} + \left(\frac{1}{4} +x_{3}\right)a \, \mathbf{\hat{z}} & \left(32e\right) & \mbox{O} \\ \mathbf{B}_{14} & = & \left(\frac{1}{2} +3x_{3}\right) \, \mathbf{a}_{1}-x_{3} \, \mathbf{a}_{2}-x_{3} \, \mathbf{a}_{3} & = & -x_{3}a \, \mathbf{\hat{x}} + \left(\frac{1}{4} +x_{3}\right)a \, \mathbf{\hat{y}} + \left(\frac{1}{4} +x_{3}\right)a \, \mathbf{\hat{z}} & \left(32e\right) & \mbox{O} \\ \end{array} \]References
- O. Knop, K. I. G. Reid, Sutarno, and Y. Nakagawa, Chalkogenides of the transition elements. VI. X–Ray, neutron, and magnetic investigation of the spinels Co3O4, NiCo2O4, Co3S4, and NiCo2S4, Can. J. Chem. 46, 3463–3476 (1968), doi:10.1139/v68-576.
- H. Hahn, G. Frank, W. Klingler, A. D. Störger, and G. Störger, Untersuchungen über Ternäre Chalkogenide. VI. Über Ternäre Chalkogenide des Aluminiums, Galliums und Indiums mit Zink, Cadmium und Quecksilber, Z. Anorg. Allg. Chem. 279, 241–270 (1955), doi:10.1002/zaac.19552790502.