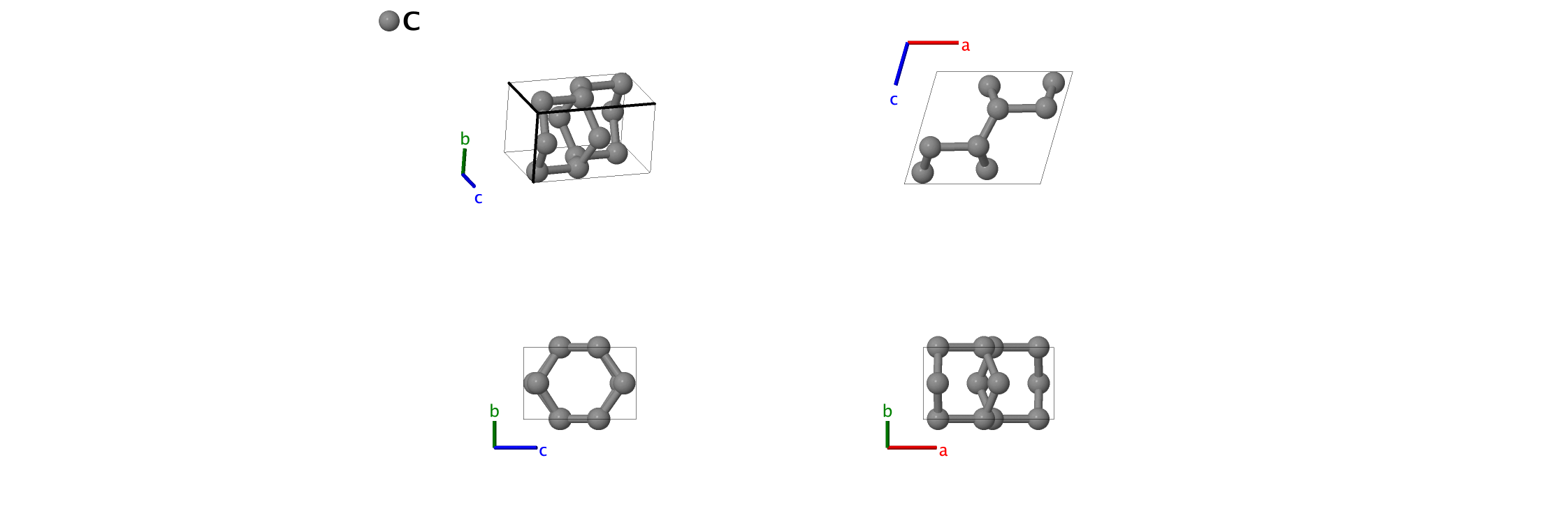
S–carbon Structure: A_mP8_10_2m2n
| Prototype | : | C |
| AFLOW prototype label | : | A_mP8_10_2m2n |
| Strukturbericht designation | : | None |
| Pearson symbol | : | mP8 |
| Space group number | : | 10 |
| Space group symbol | : | $P2/m$ |
| AFLOW prototype command | : | aflow --proto=A_mP8_10_2m2n --params=$a,b/a,c/a,\beta,x_{1},z_{1},x_{2},z_{2},x_{3},z_{3},x_{4},z_{4}$ |
- This is a predicted
superhard
allotrope of carbon. Shortly after this paper was published, two other papers predicted similar structures, differentiated mainly by an origin shift:- F–carbon (Tian, 2012): the origin is shifted by $1/2 \, \mathbf{a}_{3}$.
- J-carbon (Wang, 2012): the origin is shifted by $1/2 \left(\mathbf{a}_{1} + \mathbf{a}_{3}\right)$.
Simple Monoclinic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \\
\mathbf{a}_2 & = & b \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \cos\beta \, \mathbf{\hat{x}} + c \sin\beta \, \mathbf{\hat{z}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = & x_{1} \, \mathbf{a}_{1} + z_{1} \, \mathbf{a}_{3} & = & \left(x_{1}a+z_{1}c\cos\beta\right) \, \mathbf{\hat{x}} + z_{1}c\sin\beta \, \mathbf{\hat{z}} & \left(2m\right) & \mbox{C I} \\ \mathbf{B}_{2} & = & -x_{1} \, \mathbf{a}_{1}-z_{1} \, \mathbf{a}_{3} & = & \left(-x_{1}a-z_{1}c\cos\beta\right) \, \mathbf{\hat{x}}-z_{1}c\sin\beta \, \mathbf{\hat{z}} & \left(2m\right) & \mbox{C I} \\ \mathbf{B}_{3} & = & x_{2} \, \mathbf{a}_{1} + z_{2} \, \mathbf{a}_{3} & = & \left(x_{2}a+z_{2}c\cos\beta\right) \, \mathbf{\hat{x}} + z_{2}c\sin\beta \, \mathbf{\hat{z}} & \left(2m\right) & \mbox{C II} \\ \mathbf{B}_{4} & = & -x_{2} \, \mathbf{a}_{1}-z_{2} \, \mathbf{a}_{3} & = & \left(-x_{2}a-z_{2}c\cos\beta\right) \, \mathbf{\hat{x}}-z_{2}c\sin\beta \, \mathbf{\hat{z}} & \left(2m\right) & \mbox{C II} \\ \mathbf{B}_{5} & = & x_{3} \, \mathbf{a}_{1} + \frac{1}{2} \, \mathbf{a}_{2} + z_{3} \, \mathbf{a}_{3} & = & \left(x_{3}a+z_{3}c\cos\beta\right) \, \mathbf{\hat{x}} + \frac{1}{2}b \, \mathbf{\hat{y}} + z_{3}c\sin\beta \, \mathbf{\hat{z}} & \left(2n\right) & \mbox{C III} \\ \mathbf{B}_{6} & = & -x_{3} \, \mathbf{a}_{1} + \frac{1}{2} \, \mathbf{a}_{2}-z_{3} \, \mathbf{a}_{3} & = & \left(-x_{3}a-z_{3}c\cos\beta\right) \, \mathbf{\hat{x}} + \frac{1}{2}b \, \mathbf{\hat{y}}-z_{3}c\sin\beta \, \mathbf{\hat{z}} & \left(2n\right) & \mbox{C III} \\ \mathbf{B}_{7} & = & x_{4} \, \mathbf{a}_{1} + \frac{1}{2} \, \mathbf{a}_{2} + z_{4} \, \mathbf{a}_{3} & = & \left(x_{4}a+z_{4}c\cos\beta\right) \, \mathbf{\hat{x}} + \frac{1}{2}b \, \mathbf{\hat{y}} + z_{4}c\sin\beta \, \mathbf{\hat{z}} & \left(2n\right) & \mbox{C IV} \\ \mathbf{B}_{8} & = & -x_{4} \, \mathbf{a}_{1} + \frac{1}{2} \, \mathbf{a}_{2}-z_{4} \, \mathbf{a}_{3} & = & \left(-x_{4}a-z_{4}c\cos\beta\right) \, \mathbf{\hat{x}} + \frac{1}{2}b \, \mathbf{\hat{y}}-z_{4}c\sin\beta \, \mathbf{\hat{z}} & \left(2n\right) & \mbox{C IV} \\ \end{array} \]References
- H. Niu, X.–Q. Chen, S. Wang, D. Li, W. L. Mao, and Y. Li, Families of Superhard Crystalline Carbon Allotropes Constructed via Cold Compression of Graphite and Nanotubes, Phys. Rev. Lett. 108, 135501 (2012), doi:10.1103/PhysRevLett.108.135501.
- F. Tian, X. Dong, Z. Zhao, J. He, and H.–T. Wang, Superhard F–carbon predicted by ab initio particle–swarm optimization methodology, J. Phys.: Condens. Matter 24, 165504 (2012), doi:10.1088/0953-8984/24/16/165504.
- J.–T. Wang, C. Chen, and Y. Kawazoe, Phase conversion from graphite toward a simple monoclinic sp–carbon allotrope, J. Chem. Phys. 137, 024502 (2012), doi:10.1063/1.4732538.
- C. He, L. Sun, C. Zhang, X. Peng, K. Zhang, and J. Zhong, New superhard carbon phases between graphite and diamond, Solid State Commun. 152, 1560–1563 (2012), doi:10.1016/j.ssc.2012.05.022.
- C. He, L. Z. Sun, and J. Zhong, Prediction of superhard carbon allotropes from the segment combination method, J. Superhard Mater. 34, 386–399 (2012), doi:10.3103/S1063457612060123.
