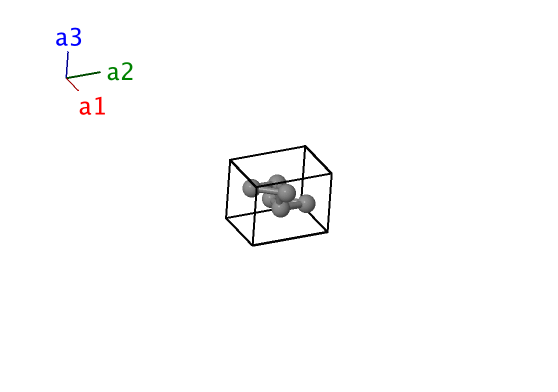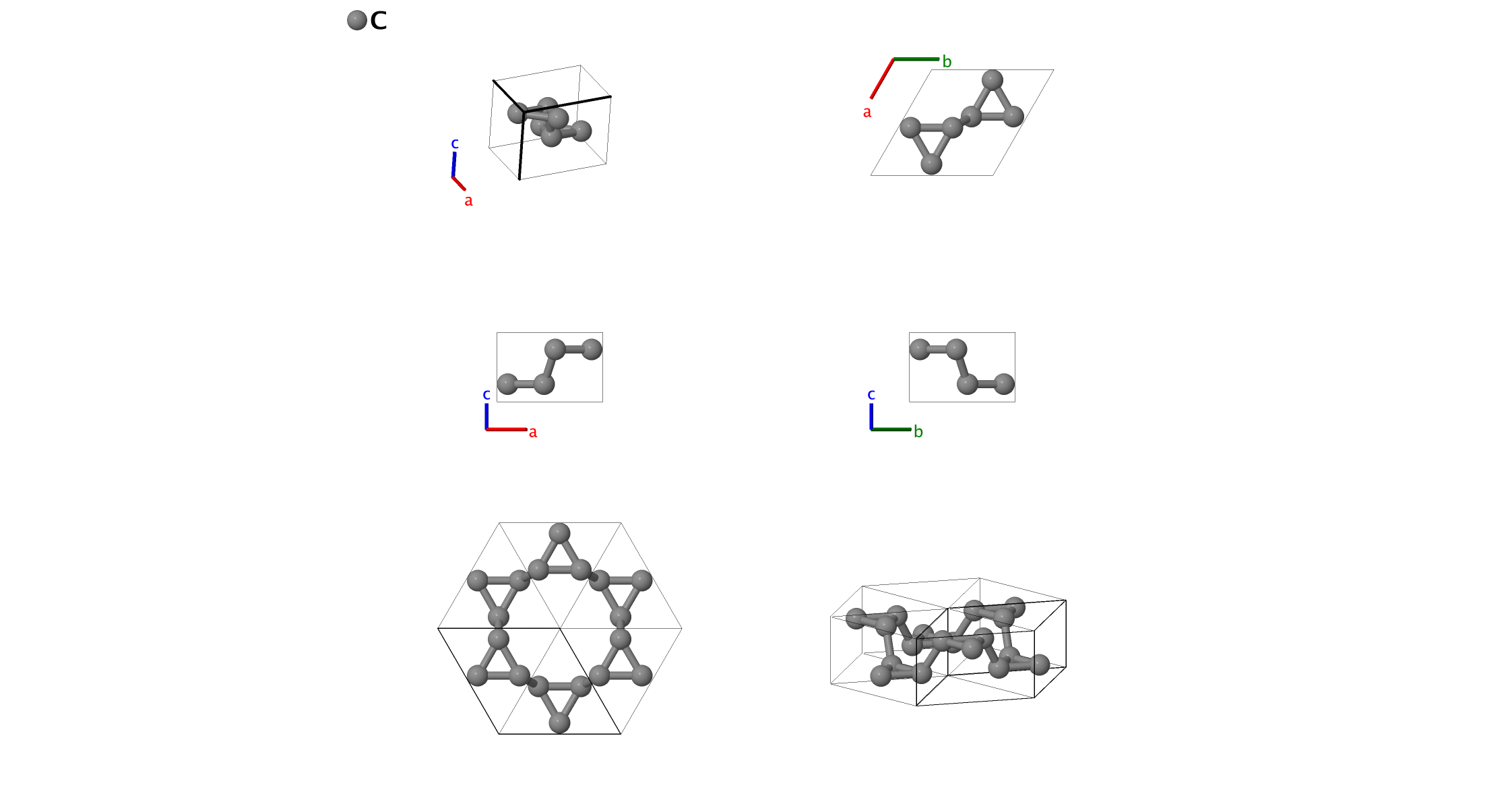
Hypothetical Tetrahedrally Bonded Carbon with 3–Member Rings: A_hP6_194_h
| Prototype | : | C |
| AFLOW prototype label | : | A_hP6_194_h |
| Strukturbericht designation | : | None |
| Pearson symbol | : | hP6 |
| Space group number | : | 194 |
| Space group symbol | : | $\mbox{P6}_{3}\mbox{/mmc}$ |
| AFLOW prototype command | : | aflow --proto=A_hP6_194_h --params=$a,c/a,x_{1}$ |
- This structure was proposed in (Schultz, 1999) to show that it was energetically possible to form three-member rings in amorphous sp$^{3}$ carbon structures.
Hexagonal primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & \frac12 \, a \, \mathbf{\hat{x}} - \frac{\sqrt3}2 \, a \, \mathbf{\hat{y}} \\
\mathbf{a}_2 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac{\sqrt3}2 \, a \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \, \mathbf{\hat{z}}\\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1}& = &x_{1} \, \mathbf{a}_{1}+ 2 \, x_{1} \, \mathbf{a}_{2}+ \frac14 \, \mathbf{a}_{3}& = &\frac32 \, x_{1} \, a \, \mathbf{\hat{x}}+ \frac{\sqrt3}{2} \, x_{1} \, a \, \mathbf{\hat{y}}+ \frac14 \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{C} \\ \mathbf{B}_{2}& = &- 2 \, x_{1} \, \mathbf{a}_{1}- x_{1} \, \mathbf{a}_{2}+ \frac14 \, \mathbf{a}_{3}& = &- \frac32 \, x_{1} \, a \, \mathbf{\hat{x}}+ \frac{\sqrt3}{2} \, x_{1} \, a \, \mathbf{\hat{y}}+ \frac14 \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{C} \\ \mathbf{B}_{3}& = &x_{1} \, \mathbf{a}_{1}- x_{1} \, \mathbf{a}_{2}+ \frac14 \, \mathbf{a}_{3}& = &- \sqrt3 \, x_{1} \, a \, \mathbf{\hat{y}}+ \frac14 \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{C} \\ \mathbf{B}_{4}& = &- x_{1} \, \mathbf{a}_{1}- 2 \, x_{1} \, \mathbf{a}_{2}+ \frac34 \, \mathbf{a}_{3}& = &- \frac32 \, x_{1} \, a \, \mathbf{\hat{x}}- \frac{\sqrt3}{2} \, x_{1} \, a \, \mathbf{\hat{y}}+ \frac34 \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{C} \\ \mathbf{B}_{5}& = &2 \, x_{1} \, \mathbf{a}_{1}+ x_{1} \, \mathbf{a}_{2}+ \frac34 \, \mathbf{a}_{3}& = &\frac32 \, x_{1} \, a \, \mathbf{\hat{x}}- \frac{\sqrt3}{2} \, x_{1} \, a \, \mathbf{\hat{y}}+ \frac34 \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{C} \\ \mathbf{B}_{6}& = &- x_{1} \, \mathbf{a}_{1}+ x_{1} \, \mathbf{a}_{2}+ \frac34 \, \mathbf{a}_{3}& = &+ \sqrt3 \, x_{1} \, a \, \mathbf{\hat{y}}+ \frac34 \, c \, \mathbf{\hat{z}}& \left(6h\right) & \mbox{C} \\ \end{array} \]References
- P. A. Schultz, K. Leung, and E. B. Stechel, Small rings and amorphous tetrahedral carbon, Phys. Rev. B 59, 733–741 (1999), doi:10.1103/PhysRevB.59.733.