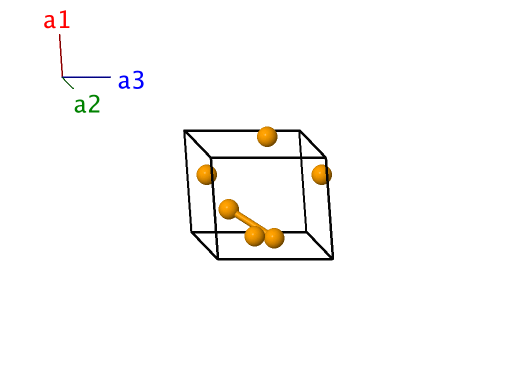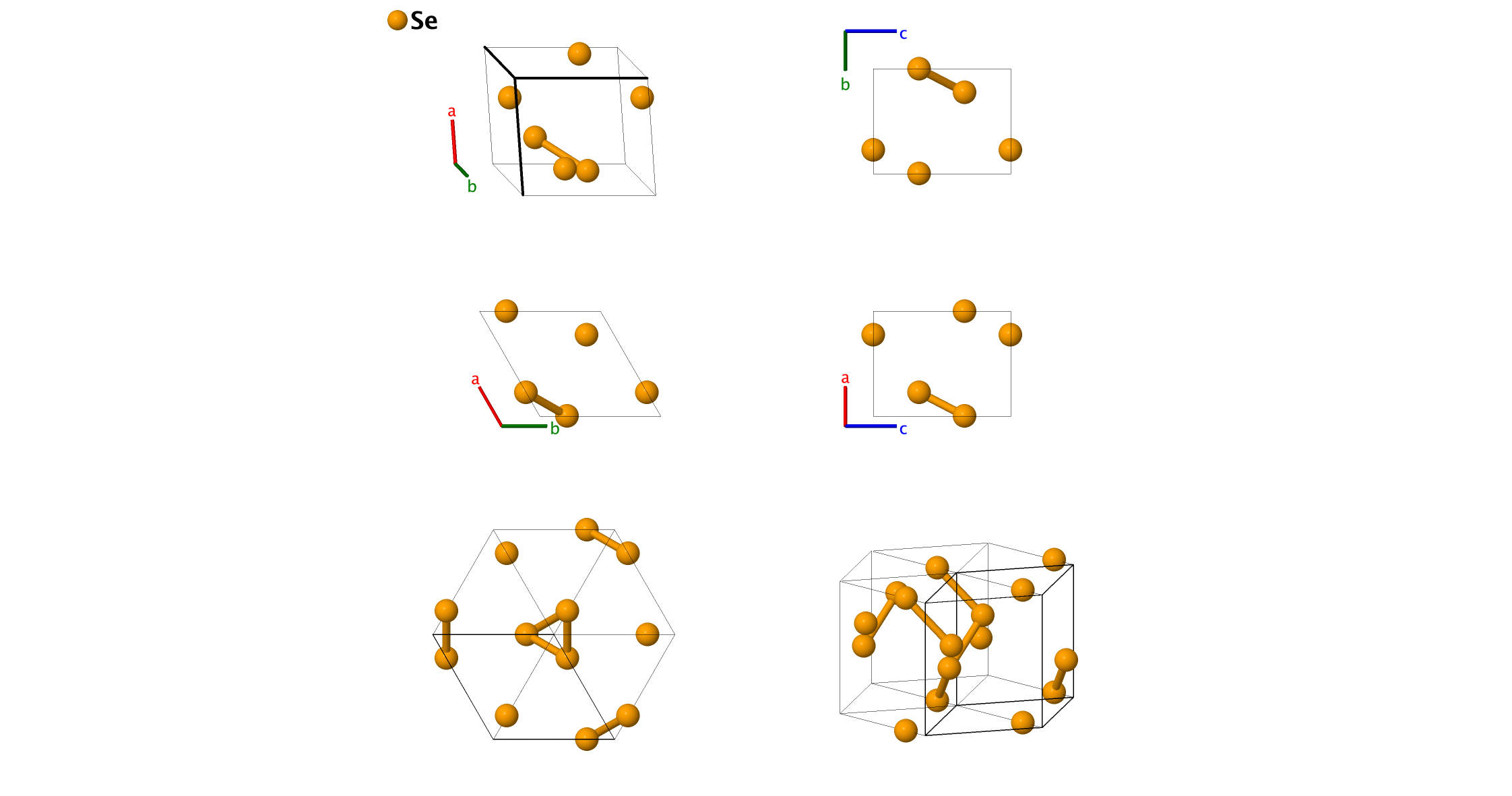
$\gamma$–Se (A8) Structure: A_hP3_152_a
| Prototype | : | $\gamma$–Se |
| AFLOW prototype label | : | A_hP3_152_a |
| Strukturbericht designation | : | $A8$ |
| Pearson symbol | : | hP3 |
| Space group number | : | 152 |
| Space group symbol | : | $\mbox{P3}_{1}\mbox{21}$ |
| AFLOW prototype command | : | aflow --proto=A_hP3_152_a --params=$a,c/a,x_{1}$ |
Other compounds with this structure
- Te, SeTe, Se3Te
- (Donohue, 1982) refers to this as the $\alpha$–Se structure, calling what we note as $\alpha$–Se and $\beta$–Se as
monoclinic $\alpha$
andmonoclinic $\beta$,
respectively. When $x = 1/3$ this reduces to the Ai ($\beta$–Po) or A10 ($\alpha$–Hg) structure. If, in addition, $c = \sqrt6 a$, then the structure becomes fcc (A1). On the other hand, if $c = \sqrt{3/2} a$, then the structure becomes simple cubic (Ah).
Trigonal Hexagonal primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & \frac12 \, a \, \mathbf{\hat{x}} - \frac{\sqrt{3}}{2} \, a \, \mathbf{\hat{y}} \\
\mathbf{a}_2 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2} \, a \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \, \mathbf{\hat{z}}\\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & =& x_{1} \, \mathbf{a}_{1} + \frac13 \, \mathbf{a}_{3}& =& \frac12 \, x_{1} \, a \, \mathbf{\hat{x}} - \frac{\sqrt3}2 \, x_{1} \, a \, \mathbf{\hat{y}} +\frac13 \, c \, \mathbf{\hat{z}}& \left(3a\right) & \mbox{Se} \\ \mathbf{B}_{2} & =& x_{1} \, \mathbf{a}_{2} + \frac23 \, \mathbf{a}_{3}& =& \frac12 \, x_{1} \, a \, \mathbf{\hat{x}} + \frac{\sqrt3}2 \, x_{1} \, a \, \mathbf{\hat{y}} +\frac23 \, c \, \mathbf{\hat{z}}& \left(3a\right) & \mbox{Se} \\ \mathbf{B}_{3} & =& - x_{1} \, \mathbf{a}_{1} - x_{1} \, \mathbf{a}_{2}& =& - x_{1} \, a \, \mathbf{\hat{x}}& \left(3a\right) & \mbox{Se} \\ \end{array} \]References
- P. Cherin and P. Unger, The Crystal Structure of Trigonal Selenium, Inorg. Chem. 6, 1589–1591 (1967), doi:10.1021/ic50054a037.
Found in
- J. Donohue, The Structure of the Elements (Robert E. Krieger Publishing Company, Malabar, Florida, 1982)., pp. 370-372 (as $\alpha$-Se).