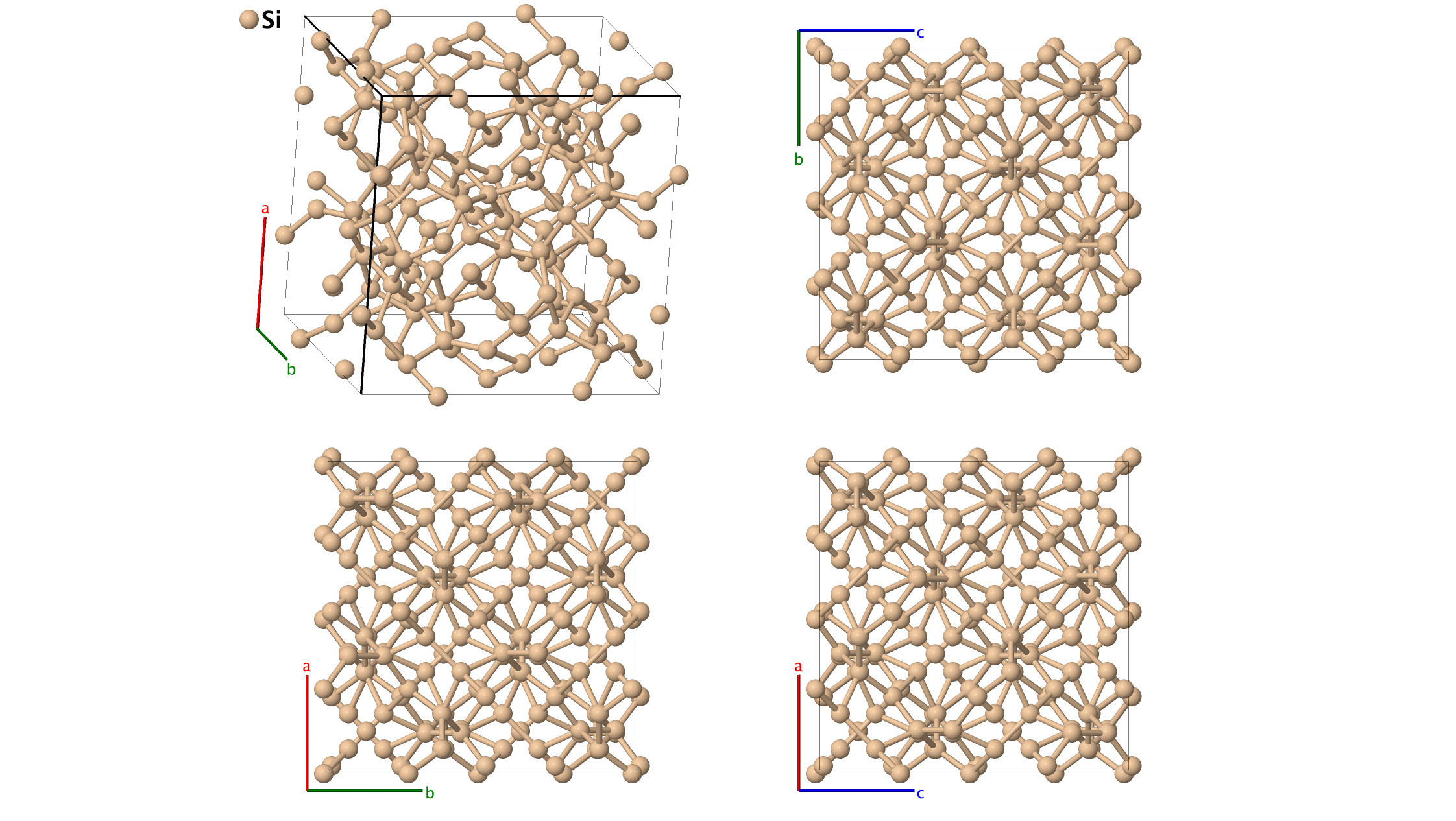
Si34 Clathrate Structure: A_cF136_227_aeg
| Prototype | : | Si |
| AFLOW prototype label | : | A_cF136_227_aeg |
| Strukturbericht designation | : | None |
| Pearson symbol | : | cF136 |
| Space group number | : | 227 |
| Space group symbol | : | $\mbox{Fd}\bar{3}\mbox{m}$ |
| AFLOW prototype command | : | aflow --proto=A_cF136_227_aeg --params=$a,x_{2},x_{3},z_{3}$ |
- Silicon clathrates are open structures of pentagonal dodecahedra connected so that all of the silicon atoms have sp$^{3}$ bonding. In nature these structures are stabilized by alkali impurity atoms. This structure and the Si46 structure are proposed
pure
silicon clathrate structures. For more information about these structures and their possible stability, see (Adams, 1994). See (Gryko, 2000) for a possible experimental realization of this structure (Si34Nax, were x is very small). We have used the fact that all vectors of the form $\left(0, \pm \, a/2, \pm \, a/2\right)$, $\left(\pm \, a/2, 0, \pm \, a/2 \right)$, and $\left( \pm \, a/2, \pm \, a/2, 0 \right)$ are primitive vectors of the face-centered cubic lattice to simplify the positions of some atoms in both lattice and Cartesian coordinates.
Face-centered Cubic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & \frac12 \, a \, \mathbf{\hat{y}} + \frac12 \, a \, \mathbf{\hat{z}} \\
\mathbf{a}_2 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, a \, \mathbf{\hat{z}} \\
\mathbf{a}_3 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, a \, \mathbf{\hat{y}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = &\frac18 \, \, \mathbf{a}_{1}+ \frac18 \, \, \mathbf{a}_{2}+ \frac18 \, \, \mathbf{a}_{3}& = &\frac18 \, a \, \mathbf{\hat{x}}+ \frac18 \, a \, \mathbf{\hat{y}}+ \frac18 \, a \, \mathbf{\hat{z}}& \left(8a\right) & \mbox{Si I} \\ \mathbf{B}_{2} & = &\frac78 \, \, \mathbf{a}_{1}+ \frac78 \, \, \mathbf{a}_{2}+ \frac78 \, \, \mathbf{a}_{3}& = &\frac78 \, a \, \mathbf{\hat{x}}+ \frac78 \, a \, \mathbf{\hat{y}}+ \frac78 \, a \, \mathbf{\hat{z}}& \left(8a\right) & \mbox{Si I} \\ \mathbf{B}_{3} & = &x_{2} \, \mathbf{a}_{1}+ x_{2} \, \mathbf{a}_{2}+ x_{2} \, \mathbf{a}_{3}& = &x_{2} \, a \, \mathbf{\hat{x}}+ x_{2} \, a \, \mathbf{\hat{y}}+ x_{2} \, a \, \mathbf{\hat{z}}& \left(32e\right) & \mbox{Si II} \\ \mathbf{B}_{4} & = &x_{2} \, \mathbf{a}_{1}+ x_{2} \, \mathbf{a}_{2}+ \left(\frac12 - 3 \, x_{2}\right) \, \mathbf{a}_{3}& = &\left(\frac14 - x_{2}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac14 - x_{2}\right) \, a \, \mathbf{\hat{y}}+ x_{2} \, a \, \mathbf{\hat{z}}& \left(32e\right) & \mbox{Si II} \\ \mathbf{B}_{5} & = &x_{2} \, \mathbf{a}_{1}+ \left(\frac12 - 3 \, x_{2}\right) \, \mathbf{a}_{2}+ x_{2} \, \mathbf{a}_{3}& = &\left(\frac14 - x_{2}\right) \, a \, \mathbf{\hat{x}}+ x_{2} \, a \, \mathbf{\hat{y}}+ \left(\frac14 - x_{2}\right) \, a \, \mathbf{\hat{z}}& \left(32e\right) & \mbox{Si II} \\ \mathbf{B}_{6} & = &\left(\frac12 - 3 \, x_{2}\right) \, \mathbf{a}_{1}+ x_{2} \, \mathbf{a}_{2}+ x_{2} \, \mathbf{a}_{3}& = &x_{2} \, a \, \mathbf{\hat{x}}+ \left(\frac14 - x_{2}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 - x_{2}\right) \, a \, \mathbf{\hat{z}}& \left(32e\right) & \mbox{Si II} \\ \mathbf{B}_{7} & = &- x_{2} \, \mathbf{a}_{1}- x_{2} \, \mathbf{a}_{2}+ \left(\frac12 + 3 \, x_{2}\right) \, \mathbf{a}_{3}& = &\left(\frac14 + x_{2}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac14 + x_{2}\right) \, a \, \mathbf{\hat{y}}- x_{2} \, a \, \mathbf{\hat{z}}& \left(32e\right) & \mbox{Si II} \\ \mathbf{B}_{8} & = &- x_{2} \, \mathbf{a}_{1}- x_{2} \, \mathbf{a}_{2}- x_{2} \, \mathbf{a}_{3}& = &- x_{2} \, a \, \mathbf{\hat{x}}- x_{2} \, a \, \mathbf{\hat{y}}- x_{2} \, a \, \mathbf{\hat{z}}& \left(32e\right) & \mbox{Si II} \\ \mathbf{B}_{9} & = &- x_{2} \, \mathbf{a}_{1}+ \left(\frac12 + 3 \, x_{2}\right) \, \mathbf{a}_{2}- x_{2} \, \mathbf{a}_{3}& = &\left(\frac14 + x_{2}\right) \, a \, \mathbf{\hat{x}}- x_{2} \, a \, \mathbf{\hat{y}}+ \left(\frac14 + x_{2}\right) \, a \, \mathbf{\hat{z}}& \left(32e\right) & \mbox{Si II} \\ \mathbf{B}_{10} & = &\left(\frac12 + 3 \, x_{2}\right) \, \mathbf{a}_{1}- x_{2} \, \mathbf{a}_{2}- x_{2} \, \mathbf{a}_{3}& = &- x_{2} \, a \, \mathbf{\hat{x}}+ \left(\frac14 + x_{2}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 + x_{2}\right) \, a \, \mathbf{\hat{z}}& \left(32e\right) & \mbox{Si II} \\ \mathbf{B}_{11} & = &z_{3} \, \mathbf{a}_{1}+ z_{3} \, \mathbf{a}_{2}+ \left(2 x_{3} - z_{3}\right) \, \mathbf{a}_{3}& = &x_{3} \, a \, \mathbf{\hat{x}}+ x_{3} \, a \, \mathbf{\hat{y}}+ z_{3} \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{12} & = &z_{3} \, \mathbf{a}_{1}+ z_{3} \, \mathbf{a}_{2}+ \left(\frac12 - 2 x_{3} - z_{3}\right) \, \mathbf{a}_{3}& = &\left(\frac14 - x_{3}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac14 - x_{3}\right) \, a \, \mathbf{\hat{y}}+ z_{3} \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{13} & = &\left(2 x_{3} - z_{3}\right) \, \mathbf{a}_{1}+ \left(\frac12 - 2 x_{3} - z_{3}\right) \, \mathbf{a}_{2}+ z_{3} \, \mathbf{a}_{3}& = &\left(\frac14 - x_{3}\right) \, a \, \mathbf{\hat{x}}+ x_{3} \, a \, \mathbf{\hat{y}}+ \left(\frac14 - z_{3}\right) \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{14} & = &\left(\frac12 - 2 x_{3} - z_{3}\right) \, \mathbf{a}_{1}+ \left(2 x_{3} - z_{3}\right) \, \mathbf{a}_{2}+ z_{3} \, \mathbf{a}_{3}& = &x_{3} \, a \, \mathbf{\hat{x}}+ \left(\frac14 - x_{3}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 - z_{3}\right) \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{15} & = &\left(2 x_{3} - z_{3}\right) \, \mathbf{a}_{1}+ z_{3} \, \mathbf{a}_{2}+ z_{3} \, \mathbf{a}_{3}& = &z_{3} \, a \, \mathbf{\hat{x}}+ x_{3} \, a \, \mathbf{\hat{y}}+ x_{3} \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{16} & = &\left(\frac12 - 2 x_{3} - z_{3}\right) \, \mathbf{a}_{1}+ z_{3} \, \mathbf{a}_{2}+ z_{3} \, \mathbf{a}_{3}& = &z_{3} \, a \, \mathbf{\hat{x}}+ \left(\frac14 - x_{3}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 - x_{3}\right) \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{17} & = &z_{3} \, \mathbf{a}_{1}+ \left(2 x_{3} - z_{3}\right) \, \mathbf{a}_{2}+ \left(\frac12 - 2 x_{3} - z_{3}\right) \, \mathbf{a}_{3}& = &\left(\frac14 - z_{3}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac14 - x_{3}\right) \, a \, \mathbf{\hat{y}}+ x_{3} \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{18} & = &z_{3} \, \mathbf{a}_{1}+ \left(\frac12 - 2 x_{3} - z_{3}\right) \, \mathbf{a}_{2}+ \left(2 x_{3} - z_{3}\right) \, \mathbf{a}_{3}& = &\left(\frac14 - z_{3}\right) \, a \, \mathbf{\hat{x}}+ x_{3} \, a \, \mathbf{\hat{y}}+ \left(\frac14 - x_{3}\right) \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{19} & = &z_{3} \, \mathbf{a}_{1}+ \left(2 x_{3} - z_{3}\right) \, \mathbf{a}_{2}+ z_{3} \, \mathbf{a}_{3}& = &x_{3} \, a \, \mathbf{\hat{x}}+ z_{3} \, a \, \mathbf{\hat{y}}+ x_{3} \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{20} & = &z_{3} \, \mathbf{a}_{1}+ \left(\frac12 - 2 x_{3} - z_{3}\right) \, \mathbf{a}_{2}+ z_{3} \, \mathbf{a}_{3}& = &\left(\frac14 - x_{3}\right) \, a \, \mathbf{\hat{x}}+ z_{3} \, a \, \mathbf{\hat{y}}+ \left(\frac14 - x_{3}\right) \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{21} & = &\left(\frac12 - 2 x_{3} - z_{3}\right) \, \mathbf{a}_{1}+ z_{3} \, \mathbf{a}_{2}+ \left(2 x_{3} - z_{3}\right) \, \mathbf{a}_{3}& = &x_{3} \, a \, \mathbf{\hat{x}}+ \left(\frac14 - z_{3}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 - x_{3}\right) \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{22} & = &\left(2 x_{3} - z_{3}\right) \, \mathbf{a}_{1}+ z_{3} \, \mathbf{a}_{2}+ \left(\frac12 - 2 x_{3} - z_{3}\right) \, \mathbf{a}_{3}& = &\left(\frac14 - x_{3}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac14 - z_{3}\right) \, a \, \mathbf{\hat{y}}+ x_{3} \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{23} & = &- z_{3} \, \mathbf{a}_{1}- z_{3} \, \mathbf{a}_{2}+ \left(\frac12 + 2 x_{3} + z_{3}\right) \, \mathbf{a}_{3}& = &\left(\frac14 + x_{3}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac14 + x_{3}\right) \, a \, \mathbf{\hat{y}}- z_{3} \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{24} & = &- z_{3} \, \mathbf{a}_{1}- z_{3} \, \mathbf{a}_{2}+ \left(z_{3} - 2 x_{3}\right) \, \mathbf{a}_{3}& = &- x_{3} \, a \, \mathbf{\hat{x}}- x_{3} \, a \, \mathbf{\hat{y}}- z_{3} \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{25} & = &\left(z_{3} - 2 x_{3}\right) \, \mathbf{a}_{1}+ \left(\frac12 + 2 x_{3} + z_{3}\right) \, \mathbf{a}_{2}- z_{3} \, \mathbf{a}_{3}& = &\left(\frac14 + x_{3}\right) \, a \, \mathbf{\hat{x}}- x_{3} \, a \, \mathbf{\hat{y}}+ \left(\frac14 + z_{3}\right) \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{26} & = &\left(\frac12 + 2 x_{3} + z_{3}\right) \, \mathbf{a}_{1}+ \left(z_{3} - 2 x_{3}\right) \, \mathbf{a}_{2}- z_{3} \, \mathbf{a}_{3}& = &- x_{3} \, a \, \mathbf{\hat{x}}+ \left(\frac14 + x_{3}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 + z_{3}\right) \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{27} & = &\left(z_{3} - 2 x_{3}\right) \, \mathbf{a}_{1}- z_{3} \, \mathbf{a}_{2}+ \left(\frac12 + 2 x_{3} + z_{3}\right) \, \mathbf{a}_{3}& = &\left(\frac14 + x_{3}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac14 + z_{3}\right) \, a \, \mathbf{\hat{y}}- x_{3} \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{28} & = &\left(\frac12 + 2 x_{3} + z_{3}\right) \, \mathbf{a}_{1}- z_{3} \, \mathbf{a}_{2}+ \left(z_{3} - 2 x_{3}\right) \, \mathbf{a}_{3}& = &- x_{3} \, a \, \mathbf{\hat{x}}+ \left(\frac14 + z_{3}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 + x_{3}\right) \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{29} & = &- z_{3} \, \mathbf{a}_{1}+ \left(z_{3} - 2 x_{3}\right) \, \mathbf{a}_{2}- z_{3} \, \mathbf{a}_{3}& = &- x_{3} \, a \, \mathbf{\hat{x}}- z_{3} \, a \, \mathbf{\hat{y}}- x_{3} \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{30} & = &- z_{3} \, \mathbf{a}_{1}+ \left(\frac12 + 2 x_{3} + z_{3}\right) \, \mathbf{a}_{2}- z_{3} \, \mathbf{a}_{3}& = &\left(\frac14 + x_{3}\right) \, a \, \mathbf{\hat{x}}- z_{3} \, a \, \mathbf{\hat{y}}+ \left(\frac14 + x_{3}\right) \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{31} & = &- z_{3} \, \mathbf{a}_{1}+ \left(z_{3} - 2 x_{3}\right) \, \mathbf{a}_{2}+ \left(\frac12 + 2 x_{3} + z_{3}\right) \, \mathbf{a}_{3}& = &\left(\frac14 + z_{3}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac14 + x_{3}\right) \, a \, \mathbf{\hat{y}}- x_{3} \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{32} & = &- z_{3} \, \mathbf{a}_{1}+ \left(\frac12 + 2 x_{3} + z_{3}\right) \, \mathbf{a}_{2}+ \left(z_{3} - 2 x_{3}\right) \, \mathbf{a}_{3}& = &\left(\frac14 + z_{3}\right) \, a \, \mathbf{\hat{x}}- x_{3} \, a \, \mathbf{\hat{y}}+ \left(\frac14 + x_{3}\right) \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{33} & = &\left(\frac12 + 2 x_{3} + z_{3}\right) \, \mathbf{a}_{1}- z_{3} \, \mathbf{a}_{2}- z_{3} \, \mathbf{a}_{3}& = &- z_{3} \, a \, \mathbf{\hat{x}}+ \left(\frac14 + x_{3}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 + x_{3}\right) \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \mathbf{B}_{34} & = &\left(z_{3} - 2 x_{3}\right) \, \mathbf{a}_{1}- z_{3} \, \mathbf{a}_{2}- z_{3} \, \mathbf{a}_{3}& = &- z_{3} \, a \, \mathbf{\hat{x}}- x_{3} \, a \, \mathbf{\hat{y}}- x_{3} \, a \, \mathbf{\hat{z}}& \left(96g\right) & \mbox{Si III} \\ \end{array} \]References
- G. B. Adams, M. O'Keeffe, A. A. Demkov, O. F. Sankey, and Y.–M. Huang, Wide–band–gap Si in open fourfold–coordinated clathrate structures, Phys. Rev. B 49, 8048–8053 (1994), doi:10.1103/PhysRevB.49.8048.
- J. Gryko, P. F. McMillan, R. F. Marzke, G. K. Ramachandran, D. Patton, S. K. Deb, and O. F. Sankey, Low–density framework form of crystalline silicon with a wide optical band gap, Phys. Rev. B 62, R7707–7710 (2000), doi:10.1103/PhysRevB.62.R7707.