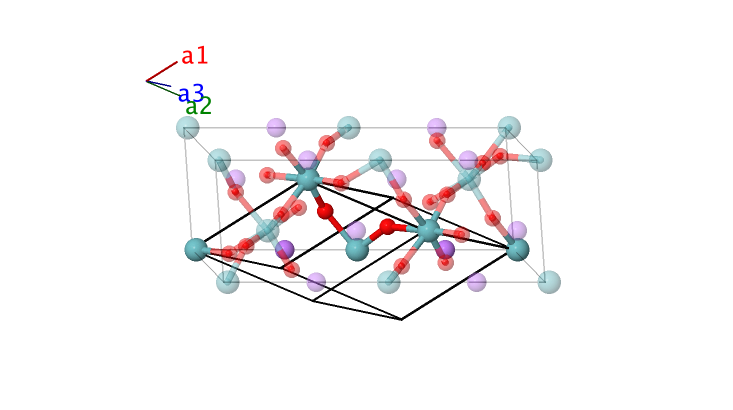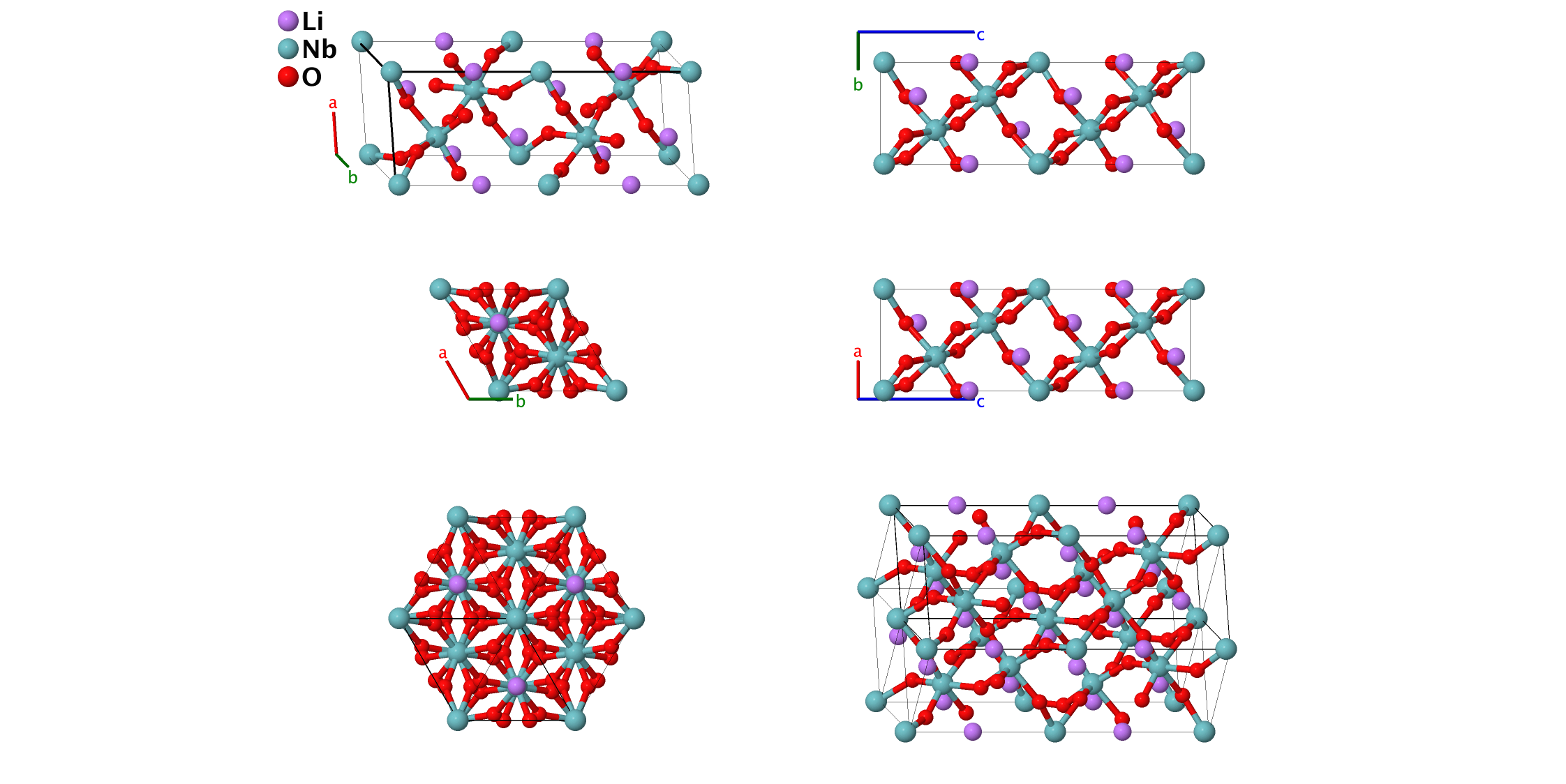
Ferroelectric LiNbO3 Structure: ABC3_hR10_161_a_a_b
| Prototype | : | LiNbO3 |
| AFLOW prototype label | : | ABC3_hR10_161_a_a_b |
| Strukturbericht designation | : | None |
| Pearson symbol | : | hR10 |
| Space group number | : | 161 |
| Space group symbol | : | $\mbox{R}3\mbox{c}$ |
| AFLOW prototype command | : | aflow --proto=ABC3_hR10_161_a_a_b [--hex] --params=$a,c/a,x_{1},x_{2},x_{3},y_{3},z_{3}$ |
- This is the ferroelectric phase of LiNbO3, which exists below 1430K. There is also a high-temperature paraelectric phase. This reduces to a double unit cell version of the cubic perovskite structure in the special case: {$c/a = \sqrt6$: This sets the angle between the rhombohedral primitive vectors to 60$^{o}$. Experimentally the value is about 56$^{o}$. {$z_{1} = 1/4$} {$z_{2} = 0$} {$x_{3} =1/2$} {$y_{3} = 0$} {$z_{3} = 0$
Rhombohedral primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & ~ \frac12 \, a \, \mathbf{\hat{x}} - \frac{1}{2\sqrt{3}} \, a \, \mathbf{\hat{y}} + \frac13
\, c \, \mathbf{\hat{z}} \\
\mathbf{a}_2 & = & \frac{1}{\sqrt{3}} \, a \, \mathbf{\hat{y}} + \frac13 \, c \, \mathbf{\hat{z}} \\
\mathbf{a}_3 & = & - \frac12 \, a \, \mathbf{\hat{x}} - \frac{1}{2\sqrt{3}} \, a \, \mathbf{\hat{y}} + \frac13
\, c \, \mathbf{\hat{z}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & =&x_{1} \, \mathbf{a}_{1}+ x_{1} \, \mathbf{a}_{2}+ x_{1} \, \mathbf{a}_{3}& =&x_{1} \, c \, \mathbf{\hat{z}}& \left(2a\right) & \mbox{Li} \\ \mathbf{B}_{2} & =&\left(\frac12 + x_{1}\right) \, \mathbf{a}_{1}+ \left(\frac12 + x_{1}\right) \, \mathbf{a}_{2}+ \left(\frac12 + x_{1}\right) \, \mathbf{a}_{3}& =&\left(\frac12 + x_{1}\right) \, c \, \mathbf{\hat{z}}& \left(2a\right) & \mbox{Li} \\ \mathbf{B}_{3} & =&x_{2} \, \mathbf{a}_{1}+ x_{2} \, \mathbf{a}_{2}+ x_{2} \, \mathbf{a}_{3}& =&x_{2} \, c \, \mathbf{\hat{z}}& \left(2a\right) & \mbox{Nb} \\ \mathbf{B}_{4} & =&\left(\frac12 + x_{2}\right) \, \mathbf{a}_{1}+ \left(\frac12 + x_{2}\right) \, \mathbf{a}_{2}+ \left(\frac12 + x_{2}\right) \, \mathbf{a}_{3}& =&\left(\frac12 + x_{2}\right) \, c \, \mathbf{\hat{z}}& \left(2a\right) & \mbox{Nb} \\ \mathbf{B}_{5} & =&x_{3} \, \mathbf{a}_{1}+ y_{3} \, \mathbf{a}_{2}+ z_{3} \, \mathbf{a}_{3}& =&\frac12 \left(x_{3} - z_{3}\right) \, a \, \mathbf{\hat{x}}- \frac1{2\sqrt3} \left(x_{3} - 2 y_{3} + z_{3}\right) \, a \, \mathbf{\hat{y}}+ \frac13 \left(x_{3} + y_{3} + z_{3}\right) \, c \, \mathbf{\hat{z}}& \left(6b\right) & \mbox{O} \\ \mathbf{B}_{6} & =&z_{3} \, \mathbf{a}_{1}+ x_{3} \, \mathbf{a}_{2}+ y_{3} \, \mathbf{a}_{3}& =&\frac12 \left(z_{3} - y_{3}\right) \, a \, \mathbf{\hat{x}}- \frac1{2\sqrt3} \left(z_{3} - 2 x_{3} + y_{3}\right) \, a \, \mathbf{\hat{y}}+ \frac13 \left(x_{3} + y_{3} + z_{3}\right) \, c \, \mathbf{\hat{z}}& \left(6b\right) & \mbox{O} \\ \mathbf{B}_{7} & =&y_{3} \, \mathbf{a}_{1}+ z_{3} \, \mathbf{a}_{2}+ x_{3} \, \mathbf{a}_{3}& =&\frac12 \left(y_{3} - x_{3}\right) \, a \, \mathbf{\hat{x}}- \frac1{2\sqrt3} \left(y_{3} - 2 z_{3} + x_{3}\right) \, a \, \mathbf{\hat{y}}+ \frac13 \left(x_{3} + y_{3} + z_{3}\right) \, c \, \mathbf{\hat{z}}& \left(6b\right) & \mbox{O} \\ \mathbf{B}_{8} & =&\left(\frac12 + y_{3}\right) \, \mathbf{a}_{1}+ \left(\frac12 + x_{3}\right) \, \mathbf{a}_{2}+ \left(\frac12 + z_{3}\right) \, \mathbf{a}_{3}& =&\frac12 \left(y_{3} - z_{3}\right) \, a \, \mathbf{\hat{x}}- \frac1{2\sqrt3} \left(z{3} - 2 x_{3} + y_{3}\right) \, a \, \mathbf{\hat{y}}+ \frac16 \left(3 + 2 x_{3} + 2 y_{3} + 2 z_{3}\right) \, c \, \mathbf{\hat{z}}& \left(6b\right) & \mbox{O} \\ \mathbf{B}_{9} & =&\left(\frac12 + x_{3}\right) \, \mathbf{a}_{1}+ \left(\frac12 + z_{3}\right) \, \mathbf{a}_{2}+ \left(\frac12 + y_{3}\right) \, \mathbf{a}_{3}& =&\frac12 \left(x_{3} - y_{3}\right) \, a \, \mathbf{\hat{x}}- \frac1{2\sqrt3} \left(y_{3} - 2 z_{3} + x_{3}\right) \, a \, \mathbf{\hat{y}}+ \frac16 \left(3 + 2 x_{3} + 2 y_{3} + 2 z_{3}\right) \, c \, \mathbf{\hat{z}}& \left(6b\right) & \mbox{O} \\ \mathbf{B}_{10} & =&\left(\frac12 + z_{3}\right) \, \mathbf{a}_{1}+ \left(\frac12 + y_{3}\right) \, \mathbf{a}_{2}+ \left(\frac12 + x_{3}\right) \, \mathbf{a}_{3}& =&\frac12 \left(z_{3} - x_{3}\right) \, a \, \mathbf{\hat{x}}- \frac1{2\sqrt3} \left(x_{3} - 2 y_{3} + z_{3}\right) \, a \, \mathbf{\hat{y}}+ \frac16 \left(3 + 2 x_{3} + 2 y_{3} + 2 z_{3}\right) \, c \, \mathbf{\hat{z}}& \left(6b\right) & \mbox{O} \\ \end{array} \]References
- H. Boysen and F. Altorfer, A neutron powder investigation of the high–temperature structure and phase transition in LiNbO3, Acta Crystallogr. Sect. B Struct. Sci. 50, 405–414 (1994), doi:10.1107/S0108768193012820.