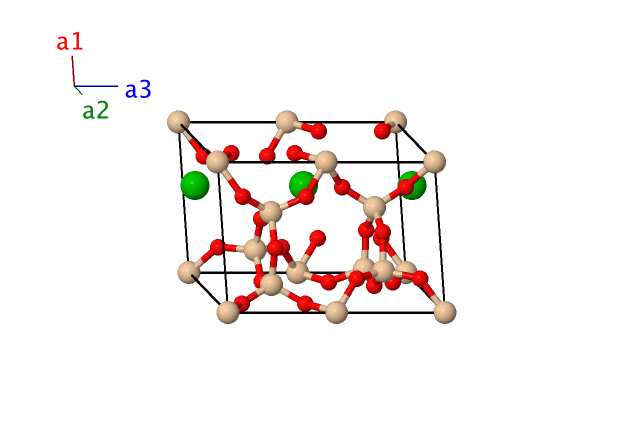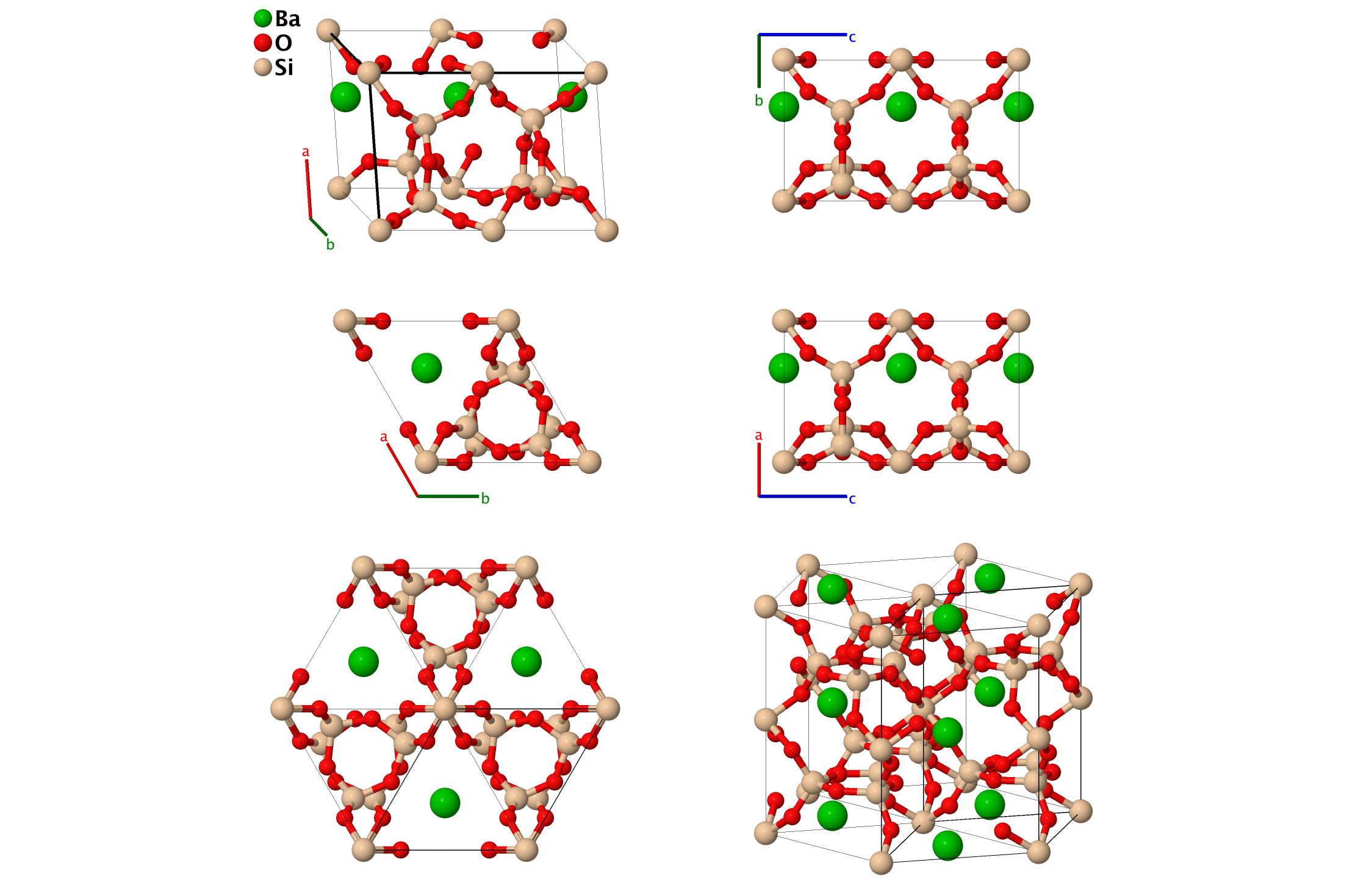
BaSi4O9 ($S3_{2}$) Structure: AB9C4_hP28_188_e_kl_ak
| Prototype | : | BaSi4O9 |
| AFLOW prototype label | : | AB9C4_hP28_188_e_kl_ak |
| Strukturbericht designation | : | $S3_{2}$ |
| Pearson symbol | : | hP28 |
| Space group number | : | 188 |
| Space group symbol | : | $P\bar{6}c2$ |
| AFLOW prototype command | : | aflow --proto=AB9C4_hP28_188_e_kl_ak --params=$a,c/a,x_{3},y_{3},x_{4},y_{4},x_{5},y_{5},z_{5}$ |
Other compounds with this structure
- BaTiSi3O9 (benitoite), Ba(SixTi1–x)Si3O9 (pabstite)
- (Hermann, 1937) applied the Strukturbericht label S32 to benitoite, BaTiSi3O9. The only difference between BaSi4O9 and benitoite is that titantium replaces silicon at the (2a) Wyckoff position.
Hexagonal primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & \frac12 \, a \, \mathbf{\hat{x}} - \frac{\sqrt3}2 \, a \, \mathbf{\hat{y}} \\
\mathbf{a}_2 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac{\sqrt3}2 \, a \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \, \mathbf{\hat{z}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = & 0 \, \mathbf{a}_{1} + 0 \, \mathbf{a}_{2} + 0 \, \mathbf{a}_{3} & = & 0 \, \mathbf{\hat{x}} + 0 \, \mathbf{\hat{y}} + 0 \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{Si I} \\ \mathbf{B}_{2} & = & \frac{1}{2} \, \mathbf{a}_{3} & = & \frac{1}{2}c \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{Si I} \\ \mathbf{B}_{3} & = & \frac{2}{3} \, \mathbf{a}_{1} + \frac{1}{3} \, \mathbf{a}_{2} & = & \frac{1}{2}a \, \mathbf{\hat{x}}- \frac{1}{2\sqrt{3}}a \, \mathbf{\hat{y}} & \left(2e\right) & \mbox{Ba} \\ \mathbf{B}_{4} & = & \frac{2}{3} \, \mathbf{a}_{1} + \frac{1}{3} \, \mathbf{a}_{2} + \frac{1}{2} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{x}}- \frac{1}{2\sqrt{3}}a \, \mathbf{\hat{y}} + \frac{1}{2}c \, \mathbf{\hat{z}} & \left(2e\right) & \mbox{Ba} \\ \mathbf{B}_{5} & = & x_{3} \, \mathbf{a}_{1} + y_{3} \, \mathbf{a}_{2} + \frac{1}{4} \, \mathbf{a}_{3} & = & \frac{1}{2}\left(x_{3}+y_{3}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}\left(-x_{3}+y_{3}\right)a \, \mathbf{\hat{y}} + \frac{1}{4}c \, \mathbf{\hat{z}} & \left(6k\right) & \mbox{O I} \\ \mathbf{B}_{6} & = & -y_{3} \, \mathbf{a}_{1} + \left(x_{3}-y_{3}\right) \, \mathbf{a}_{2} + \frac{1}{4} \, \mathbf{a}_{3} & = & \left(\frac{1}{2}x_{3}-y_{3}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}x_{3}a \, \mathbf{\hat{y}} + \frac{1}{4}c \, \mathbf{\hat{z}} & \left(6k\right) & \mbox{O I} \\ \mathbf{B}_{7} & = & \left(-x_{3}+y_{3}\right) \, \mathbf{a}_{1}-x_{3} \, \mathbf{a}_{2} + \frac{1}{4} \, \mathbf{a}_{3} & = & \left(-x_{3}+\frac{1}{2}y_{3}\right)a \, \mathbf{\hat{x}}-\frac{\sqrt{3}}{2}y_{3}a \, \mathbf{\hat{y}} + \frac{1}{4}c \, \mathbf{\hat{z}} & \left(6k\right) & \mbox{O I} \\ \mathbf{B}_{8} & = & -y_{3} \, \mathbf{a}_{1}-x_{3} \, \mathbf{a}_{2} + \frac{3}{4} \, \mathbf{a}_{3} & = & -\frac{1}{2}\left(x_{3}+y_{3}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}\left(-x_{3}+y_{3}\right)a \, \mathbf{\hat{y}} + \frac{3}{4}c \, \mathbf{\hat{z}} & \left(6k\right) & \mbox{O I} \\ \mathbf{B}_{9} & = & \left(-x_{3}+y_{3}\right) \, \mathbf{a}_{1} + y_{3} \, \mathbf{a}_{2} + \frac{3}{4} \, \mathbf{a}_{3} & = & \left(-\frac{1}{2}x_{3}+y_{3}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}x_{3}a \, \mathbf{\hat{y}} + \frac{3}{4}c \, \mathbf{\hat{z}} & \left(6k\right) & \mbox{O I} \\ \mathbf{B}_{10} & = & x_{3} \, \mathbf{a}_{1} + \left(x_{3}-y_{3}\right) \, \mathbf{a}_{2} + \frac{3}{4} \, \mathbf{a}_{3} & = & \left(x_{3}-\frac{1}{2}y_{3}\right)a \, \mathbf{\hat{x}}-\frac{\sqrt{3}}{2}y_{3}a \, \mathbf{\hat{y}} + \frac{3}{4}c \, \mathbf{\hat{z}} & \left(6k\right) & \mbox{O I} \\ \mathbf{B}_{11} & = & x_{4} \, \mathbf{a}_{1} + y_{4} \, \mathbf{a}_{2} + \frac{1}{4} \, \mathbf{a}_{3} & = & \frac{1}{2}\left(x_{4}+y_{4}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}\left(-x_{4}+y_{4}\right)a \, \mathbf{\hat{y}} + \frac{1}{4}c \, \mathbf{\hat{z}} & \left(6k\right) & \mbox{Si II} \\ \mathbf{B}_{12} & = & -y_{4} \, \mathbf{a}_{1} + \left(x_{4}-y_{4}\right) \, \mathbf{a}_{2} + \frac{1}{4} \, \mathbf{a}_{3} & = & \left(\frac{1}{2}x_{4}-y_{4}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}x_{4}a \, \mathbf{\hat{y}} + \frac{1}{4}c \, \mathbf{\hat{z}} & \left(6k\right) & \mbox{Si II} \\ \mathbf{B}_{13} & = & \left(-x_{4}+y_{4}\right) \, \mathbf{a}_{1}-x_{4} \, \mathbf{a}_{2} + \frac{1}{4} \, \mathbf{a}_{3} & = & \left(-x_{4}+\frac{1}{2}y_{4}\right)a \, \mathbf{\hat{x}}-\frac{\sqrt{3}}{2}y_{4}a \, \mathbf{\hat{y}} + \frac{1}{4}c \, \mathbf{\hat{z}} & \left(6k\right) & \mbox{Si II} \\ \mathbf{B}_{14} & = & -y_{4} \, \mathbf{a}_{1}-x_{4} \, \mathbf{a}_{2} + \frac{3}{4} \, \mathbf{a}_{3} & = & -\frac{1}{2}\left(x_{4}+y_{4}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}\left(-x_{4}+y_{4}\right)a \, \mathbf{\hat{y}} + \frac{3}{4}c \, \mathbf{\hat{z}} & \left(6k\right) & \mbox{Si II} \\ \mathbf{B}_{15} & = & \left(-x_{4}+y_{4}\right) \, \mathbf{a}_{1} + y_{4} \, \mathbf{a}_{2} + \frac{3}{4} \, \mathbf{a}_{3} & = & \left(-\frac{1}{2}x_{4}+y_{4}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}x_{4}a \, \mathbf{\hat{y}} + \frac{3}{4}c \, \mathbf{\hat{z}} & \left(6k\right) & \mbox{Si II} \\ \mathbf{B}_{16} & = & x_{4} \, \mathbf{a}_{1} + \left(x_{4}-y_{4}\right) \, \mathbf{a}_{2} + \frac{3}{4} \, \mathbf{a}_{3} & = & \left(x_{4}-\frac{1}{2}y_{4}\right)a \, \mathbf{\hat{x}}-\frac{\sqrt{3}}{2}y_{4}a \, \mathbf{\hat{y}} + \frac{3}{4}c \, \mathbf{\hat{z}} & \left(6k\right) & \mbox{Si II} \\ \mathbf{B}_{17} & = & x_{5} \, \mathbf{a}_{1} + y_{5} \, \mathbf{a}_{2} + z_{5} \, \mathbf{a}_{3} & = & \frac{1}{2}\left(x_{5}+y_{5}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}\left(-x_{5}+y_{5}\right)a \, \mathbf{\hat{y}} + z_{5}c \, \mathbf{\hat{z}} & \left(12l\right) & \mbox{O II} \\ \mathbf{B}_{18} & = & -y_{5} \, \mathbf{a}_{1} + \left(x_{5}-y_{5}\right) \, \mathbf{a}_{2} + z_{5} \, \mathbf{a}_{3} & = & \left(\frac{1}{2}x_{5}-y_{5}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}x_{5}a \, \mathbf{\hat{y}} + z_{5}c \, \mathbf{\hat{z}} & \left(12l\right) & \mbox{O II} \\ \mathbf{B}_{19} & = & \left(-x_{5}+y_{5}\right) \, \mathbf{a}_{1}-x_{5} \, \mathbf{a}_{2} + z_{5} \, \mathbf{a}_{3} & = & \left(-x_{5}+\frac{1}{2}y_{5}\right)a \, \mathbf{\hat{x}}-\frac{\sqrt{3}}{2}y_{5}a \, \mathbf{\hat{y}} + z_{5}c \, \mathbf{\hat{z}} & \left(12l\right) & \mbox{O II} \\ \mathbf{B}_{20} & = & x_{5} \, \mathbf{a}_{1} + y_{5} \, \mathbf{a}_{2} + \left(\frac{1}{2} - z_{5}\right) \, \mathbf{a}_{3} & = & \frac{1}{2}\left(x_{5}+y_{5}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}\left(-x_{5}+y_{5}\right)a \, \mathbf{\hat{y}} + \left(\frac{1}{2} - z_{5}\right)c \, \mathbf{\hat{z}} & \left(12l\right) & \mbox{O II} \\ \mathbf{B}_{21} & = & -y_{5} \, \mathbf{a}_{1} + \left(x_{5}-y_{5}\right) \, \mathbf{a}_{2} + \left(\frac{1}{2} - z_{5}\right) \, \mathbf{a}_{3} & = & \left(\frac{1}{2}x_{5}-y_{5}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}x_{5}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} - z_{5}\right)c \, \mathbf{\hat{z}} & \left(12l\right) & \mbox{O II} \\ \mathbf{B}_{22} & = & \left(-x_{5}+y_{5}\right) \, \mathbf{a}_{1}-x_{5} \, \mathbf{a}_{2} + \left(\frac{1}{2} - z_{5}\right) \, \mathbf{a}_{3} & = & \left(-x_{5}+\frac{1}{2}y_{5}\right)a \, \mathbf{\hat{x}}-\frac{\sqrt{3}}{2}y_{5}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} - z_{5}\right)c \, \mathbf{\hat{z}} & \left(12l\right) & \mbox{O II} \\ \mathbf{B}_{23} & = & -y_{5} \, \mathbf{a}_{1}-x_{5} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{5}\right) \, \mathbf{a}_{3} & = & -\frac{1}{2}\left(x_{5}+y_{5}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}\left(-x_{5}+y_{5}\right)a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{5}\right)c \, \mathbf{\hat{z}} & \left(12l\right) & \mbox{O II} \\ \mathbf{B}_{24} & = & \left(-x_{5}+y_{5}\right) \, \mathbf{a}_{1} + y_{5} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{5}\right) \, \mathbf{a}_{3} & = & \left(-\frac{1}{2}x_{5}+y_{5}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}x_{5}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{5}\right)c \, \mathbf{\hat{z}} & \left(12l\right) & \mbox{O II} \\ \mathbf{B}_{25} & = & x_{5} \, \mathbf{a}_{1} + \left(x_{5}-y_{5}\right) \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{5}\right) \, \mathbf{a}_{3} & = & \left(x_{5}-\frac{1}{2}y_{5}\right)a \, \mathbf{\hat{x}}-\frac{\sqrt{3}}{2}y_{5}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{5}\right)c \, \mathbf{\hat{z}} & \left(12l\right) & \mbox{O II} \\ \mathbf{B}_{26} & = & -y_{5} \, \mathbf{a}_{1}-x_{5} \, \mathbf{a}_{2}-z_{5} \, \mathbf{a}_{3} & = & -\frac{1}{2}\left(x_{5}+y_{5}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}\left(-x_{5}+y_{5}\right)a \, \mathbf{\hat{y}}-z_{5}c \, \mathbf{\hat{z}} & \left(12l\right) & \mbox{O II} \\ \mathbf{B}_{27} & = & \left(-x_{5}+y_{5}\right) \, \mathbf{a}_{1} + y_{5} \, \mathbf{a}_{2}-z_{5} \, \mathbf{a}_{3} & = & \left(-\frac{1}{2}x_{5}+y_{5}\right)a \, \mathbf{\hat{x}} + \frac{\sqrt{3}}{2}x_{5}a \, \mathbf{\hat{y}}-z_{5}c \, \mathbf{\hat{z}} & \left(12l\right) & \mbox{O II} \\ \mathbf{B}_{28} & = & x_{5} \, \mathbf{a}_{1} + \left(x_{5}-y_{5}\right) \, \mathbf{a}_{2}-z_{5} \, \mathbf{a}_{3} & = & \left(x_{5}-\frac{1}{2}y_{5}\right)a \, \mathbf{\hat{x}}-\frac{\sqrt{3}}{2}y_{5}a \, \mathbf{\hat{y}}-z_{5}c \, \mathbf{\hat{z}} & \left(12l\right) & \mbox{O II} \\ \end{array} \]References
- L. W. Finger, R. M. Hazen, and B. A. Fursenko, Refinement of the crystal structure of BaSi4O9 in the benitoite form, J. Phys. Chem. Solids 56, 1389–1393 (1995), doi:10.1016/0022-3697(95)00075-5.
- C. Hermann, O. Lohrmann, and H. Philipp, eds., Strukturbericht Band II, 1928–1932 (Akademische Verlagsgesellschaft M. B. H., Leipzig, 1937).
Found in
- P. Villars and K. Cenzual, Pearson's Crystal Data – Crystal Structure Database for Inorganic Compounds, ASM International (2013).