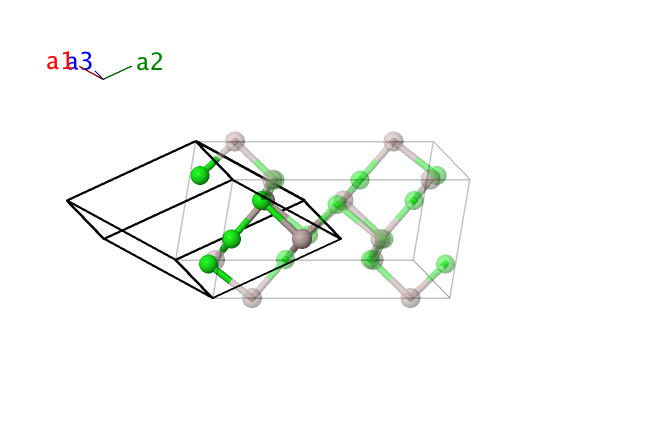
AlCl3 (D015) Structure: AB3_mC16_12_g_ij
| Prototype | : | AlCl3 |
| AFLOW prototype label | : | AB3_mC16_12_g_ij |
| Strukturbericht designation | : | $D0_{15}$ |
| Pearson symbol | : | mC16 |
| Space group number | : | 12 |
| Space group symbol | : | $\mbox{C2/m}$ |
| AFLOW prototype command | : | aflow --proto=AB3_mC16_12_g_ij --params=$a,b/a,c/a,\beta,y_{1},x_{2},z_{2},x_{3},y_{3},z_{3}$ |
Other compounds with this structure
- DyCl3, ErCl3, HoCl3, InCl3, LuCl3, TlCl3, TmCl3, YbCl3
- This structure has a somewhat complicated history. Strukturbericht Volume II lists the space group as either P3112 or P3212. This structure was later refined by Ketelaar in space group C2/m. See (Villars, 2008) for more information.
Base-centered Monoclinic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & \frac12 \, a \, \mathbf{\hat{x}} - \frac12 \, b \, \mathbf{\hat{y}} \\
\mathbf{a}_2 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, b \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \cos\beta \, \mathbf{\hat{x}} + c \sin\beta \, \mathbf{\hat{z}}
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & =& - y_{1} \, \mathbf{a}_{1} + y_{1} \, \mathbf{a}_{2}& =& y_{1} \, b \, \mathbf{\hat{y}}& \left(4g\right) & \mbox{Al} \\ \mathbf{B}_{2} & =& y_{1} \, \mathbf{a}_{1} - y_{1} \, \mathbf{a}_{2}& =& - y_{1} \, b \, \mathbf{\hat{y}}& \left(4g\right) & \mbox{Al} \\ \mathbf{B}_{3} & =& x_{2} \, \mathbf{a}_{1} + x_{2} \, \mathbf{a}_{2} + z_{2} \, \mathbf{a}_{3}& =& \left(x_{2} \, a + z_{2} \, c \, \cos\beta\right) \, \mathbf{\hat{x}}+ z_{2} \, c \, \sin\beta \, \mathbf{\hat{z}}& \left(4i\right) & \mbox{Cl I} \\ \mathbf{B}_{4} & =& - x_{2} \, \mathbf{a}_{1} - x_{2} \, \mathbf{a}_{2} - z_{2} \, \mathbf{a}_{3}& =& - \left(x_{2} \, a + z_2 \, c \, \cos\beta\right) \, \mathbf{\hat{x}}- z_2 \, c \, \sin\beta \, \mathbf{\hat{z}}& \left(4i\right) & \mbox{Cl I} \\ \mathbf{B}_{5} & =& \left(x_{3} - y_{3}\right) \, \mathbf{a}_{1} + \left(x_{3} + y_{3}\right) \, \mathbf{a}_{2} + z_{3} \, \mathbf{a}_{3}& =& \left(x_{3} \, a + z_{3} \, c \, \cos\beta\right) \, \mathbf{\hat{x}}+ y_{3} \, b \, \mathbf{\hat{y}}+ z_{3} \, c \, \sin\beta \, \mathbf{\hat{z}}& \left(8j\right) & \mbox{Cl II} \\ \mathbf{B}_{6} & =& -\left(x_{3} + y_{3}\right) \, \mathbf{a}_{1} + \left(y_{3} - x_{3}\right) \, \mathbf{a}_{2} - z_{3} \, \mathbf{a}_{3}& =& - \left(x_{3} \, a + z_{3} \, c \, \cos\beta\right) \, \mathbf{\hat{x}}+ y_{3} \, b \, \mathbf{\hat{y}}- z_{3} \, c \, \sin\beta \, \mathbf{\hat{z}}& \left(8j\right) & \mbox{Cl II} \\ \mathbf{B}_{7} & =& \left(y_{3} - x_{3}\right) \, \mathbf{a}_{1} - \left(x_{3} + y_{3}\right) \, \mathbf{a}_{2} - z_{3} \, \mathbf{a}_{3}& =& - \left(x_{3} \, a + z_{3} \, c \, \cos\beta\right) \, \mathbf{\hat{x}}- y_{3} \, b \, \mathbf{\hat{y}}- z_{3} \, c \, \sin\beta \, \mathbf{\hat{z}}& \left(8j\right) & \mbox{Cl II} \\ \mathbf{B}_{8} & =& \left(x_{3} + y_{3}\right) \, \mathbf{a}_{1} + \left(x_{3} - y_{3}\right) \, \mathbf{a}_{2} + z_{3} \, \mathbf{a}_{3}& =& \left(x_{3} \, a + z_{3} \, c \, \cos\beta\right) \, \mathbf{\hat{x}}- y_{3} \, b \, \mathbf{\hat{y}}+ z_{3} \, c \, \sin\beta \, \mathbf{\hat{z}}& \left(8j\right) & \mbox{Cl II} \\ \end{array} \]References
- S. I. Troyanov, The crystal structure of titanium(II) tetrachloroaluminate Ti(AlCl4)2 and refinement of the crystal structure of AlCl3, (Russian) Journal of Inorganic Chemistry (translated from Zhurnal Neorganicheskoi Khimii) 37, 121–124 (1992).
- C. Hermann, O. Lohrmann, and H. Philipp, Strukturbericht Band II, 1928–1932 (Akademsiche Verlagsgesellschaft M. B. H., Leipzig, 1937).
- P. Villars, K. Cenzual, J. Daams, R. Gladyshevskii, O. Shcherban, V. Dubenskyy, N. Melnichenko–Koblyuk, O. Pavlyuk, I. Savesyuk, S. Stoiko, and L. Sysa, Landolt–Börnstein – Group III Condensed Matter (Springer–Verlag GmbH, Heidelberg, 2008). Accessed through the Springer Materials site.
Found in
- P. Villars, Material Phases Data System ((MPDS), CH–6354 Vitznau, Switzerland, 2014). Accessed through the Springer Materials site.