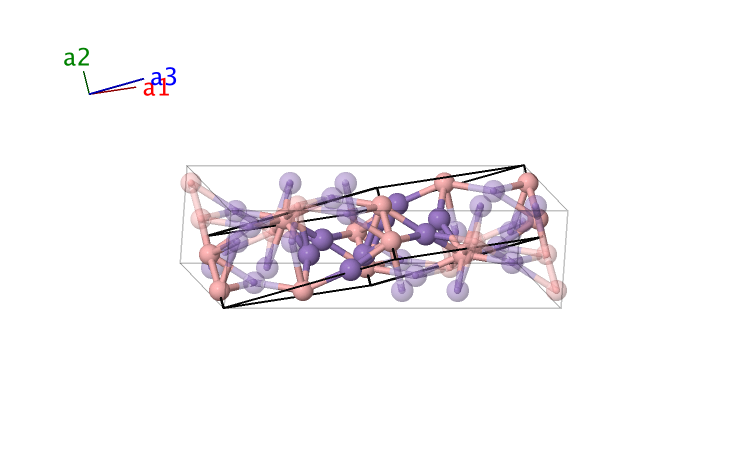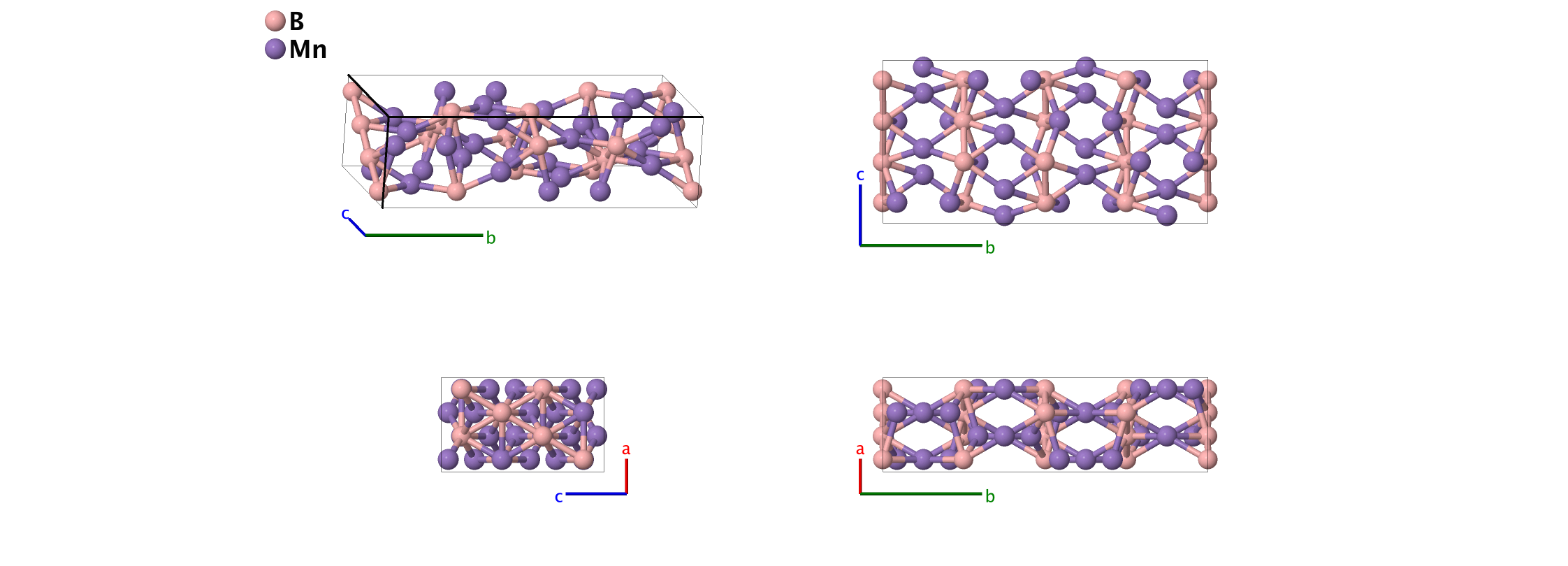
Mn2B ($D1_{f}$) Structure: AB2_oF48_70_f_fg
| Prototype | : | Mn2B |
| AFLOW prototype label | : | AB2_oF48_70_f_fg |
| Strukturbericht designation | : | $D1_{f}$ |
| Pearson symbol | : | oF48 |
| Space group number | : | 70 |
| Space group symbol | : | $Fddd$ |
| AFLOW prototype command | : | aflow --proto=AB2_oF48_70_f_fg --params=$a,b/a,c/a,y_{1},y_{2},z_{3}$ |
Other compounds with this structure
- Cr2B
- Early works, {\em e.g.} (Pearson, 1958) referred to this structure as Mn4B, with the same space group and Wyckoff positions. The stoichiometry was fixed by assuming that the (16e) boron positions were only half-occupied. Tergenius's 1981 refinement of the structure showed that the (16e) sites were totally filled, fixing the stoichiometry to Mn2B. A similar reanalysis showed that the similar structure known has Cr4B also had composition Cr2B. Tergenius gives the atomic positions using the first setting of space group $Fddd$ #70. We have translated this into the second setting, where the origin is on an inversion site. As a part of this process the primitive axes were also rotated compared to Tergenius.
Face-centered Orthorhombic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & \frac12 \, b \, \mathbf{\hat{y}} + \frac12 \, c \, \mathbf{\hat{z}} \\
\mathbf{a}_2 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, c \, \mathbf{\hat{z}} \\
\mathbf{a}_3 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, b \, \mathbf{\hat{y}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = & y_{1} \, \mathbf{a}_{1} + \left(\frac{1}{4} - y_{1}\right) \, \mathbf{a}_{2} + y_{1} \, \mathbf{a}_{3} & = & \frac{1}{8}a \, \mathbf{\hat{x}} + y_{1}b \, \mathbf{\hat{y}} + \frac{1}{8}c \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{B} \\ \mathbf{B}_{2} & = & \left(\frac{1}{4} - y_{1}\right) \, \mathbf{a}_{1} + y_{1} \, \mathbf{a}_{2} + \left(\frac{1}{4} - y_{1}\right) \, \mathbf{a}_{3} & = & \frac{1}{8}a \, \mathbf{\hat{x}} + \left(\frac{1}{4} - y_{1}\right)b \, \mathbf{\hat{y}} + \frac{1}{8}c \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{B} \\ \mathbf{B}_{3} & = & -y_{1} \, \mathbf{a}_{1} + \left(\frac{3}{4} +y_{1}\right) \, \mathbf{a}_{2}-y_{1} \, \mathbf{a}_{3} & = & \frac{3}{8}a \, \mathbf{\hat{x}}-y_{1}b \, \mathbf{\hat{y}} + \frac{3}{8}c \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{B} \\ \mathbf{B}_{4} & = & \left(\frac{3}{4} +y_{1}\right) \, \mathbf{a}_{1}-y_{1} \, \mathbf{a}_{2} + \left(\frac{3}{4} +y_{1}\right) \, \mathbf{a}_{3} & = & \frac{3}{8}a \, \mathbf{\hat{x}} + \left(\frac{3}{4} +y_{1}\right)b \, \mathbf{\hat{y}} + \frac{3}{8}c \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{B} \\ \mathbf{B}_{5} & = & y_{2} \, \mathbf{a}_{1} + \left(\frac{1}{4} - y_{2}\right) \, \mathbf{a}_{2} + y_{2} \, \mathbf{a}_{3} & = & \frac{1}{8}a \, \mathbf{\hat{x}} + y_{2}b \, \mathbf{\hat{y}} + \frac{1}{8}c \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Mn I} \\ \mathbf{B}_{6} & = & \left(\frac{1}{4} - y_{2}\right) \, \mathbf{a}_{1} + y_{2} \, \mathbf{a}_{2} + \left(\frac{1}{4} - y_{2}\right) \, \mathbf{a}_{3} & = & \frac{1}{8}a \, \mathbf{\hat{x}} + \left(\frac{1}{4} - y_{2}\right)b \, \mathbf{\hat{y}} + \frac{1}{8}c \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Mn I} \\ \mathbf{B}_{7} & = & -y_{2} \, \mathbf{a}_{1} + \left(\frac{3}{4} +y_{2}\right) \, \mathbf{a}_{2}-y_{2} \, \mathbf{a}_{3} & = & \frac{3}{8}a \, \mathbf{\hat{x}}-y_{2}b \, \mathbf{\hat{y}} + \frac{3}{8}c \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Mn I} \\ \mathbf{B}_{8} & = & \left(\frac{3}{4} +y_{2}\right) \, \mathbf{a}_{1}-y_{2} \, \mathbf{a}_{2} + \left(\frac{3}{4} +y_{2}\right) \, \mathbf{a}_{3} & = & \frac{3}{8}a \, \mathbf{\hat{x}} + \left(\frac{3}{4} +y_{2}\right)b \, \mathbf{\hat{y}} + \frac{3}{8}c \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Mn I} \\ \mathbf{B}_{9} & = & z_{3} \, \mathbf{a}_{1} + z_{3} \, \mathbf{a}_{2} + \left(\frac{1}{4} - z_{3}\right) \, \mathbf{a}_{3} & = & \frac{1}{8}a \, \mathbf{\hat{x}} + \frac{1}{8}b \, \mathbf{\hat{y}} + z_{3}c \, \mathbf{\hat{z}} & \left(16g\right) & \mbox{Mn II} \\ \mathbf{B}_{10} & = & \left(\frac{1}{4} - z_{3}\right) \, \mathbf{a}_{1} + \left(\frac{1}{4} - z_{3}\right) \, \mathbf{a}_{2} + z_{3} \, \mathbf{a}_{3} & = & \frac{1}{8}a \, \mathbf{\hat{x}} + \frac{1}{8}b \, \mathbf{\hat{y}} + \left(\frac{1}{4} - z_{3}\right)c \, \mathbf{\hat{z}} & \left(16g\right) & \mbox{Mn II} \\ \mathbf{B}_{11} & = & -z_{3} \, \mathbf{a}_{1}-z_{3} \, \mathbf{a}_{2} + \left(\frac{3}{4} +z_{3}\right) \, \mathbf{a}_{3} & = & \frac{3}{8}a \, \mathbf{\hat{x}} + \frac{3}{8}b \, \mathbf{\hat{y}}-z_{3}c \, \mathbf{\hat{z}} & \left(16g\right) & \mbox{Mn II} \\ \mathbf{B}_{12} & = & \left(\frac{3}{4} +z_{3}\right) \, \mathbf{a}_{1} + \left(\frac{3}{4} +z_{3}\right) \, \mathbf{a}_{2}-z_{3} \, \mathbf{a}_{3} & = & \frac{3}{8}a \, \mathbf{\hat{x}} + \frac{3}{8}b \, \mathbf{\hat{y}} + \left(\frac{3}{4} +z_{3}\right)c \, \mathbf{\hat{z}} & \left(16g\right) & \mbox{Mn II} \\ \end{array} \]References
- L.–E. Tergenius, Refinement of the crystal structure of orthorhombic Mn2B (formerly denoted Mn4B), J. Less–Common Met. 82, 335–340 (1981), doi:10.1016/0022-5088(81)90236-8.
- W. B. Pearson, A Handbook of Lattice Spacings and Structures of Metals and Alloys, no. N.R.C. No. 4303 in International Series of Monographs on Metal Physics and Physical Metallurgy (Pergamon Press, Oxford, London, Edinburgh, New York, Paris, Frankfort, 1958), 1964 reprint with corrections edn.