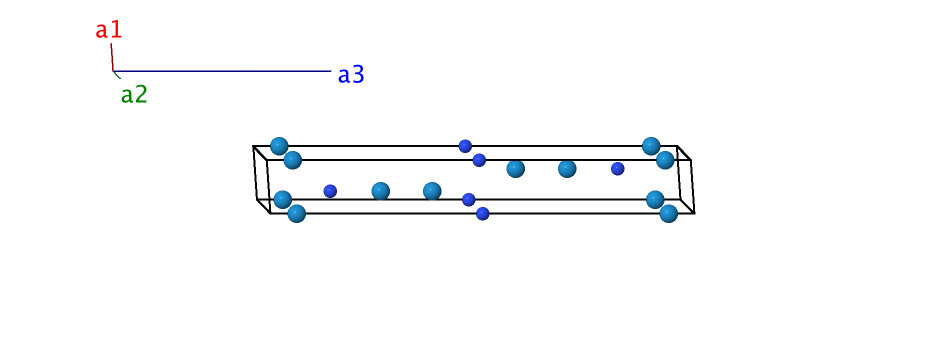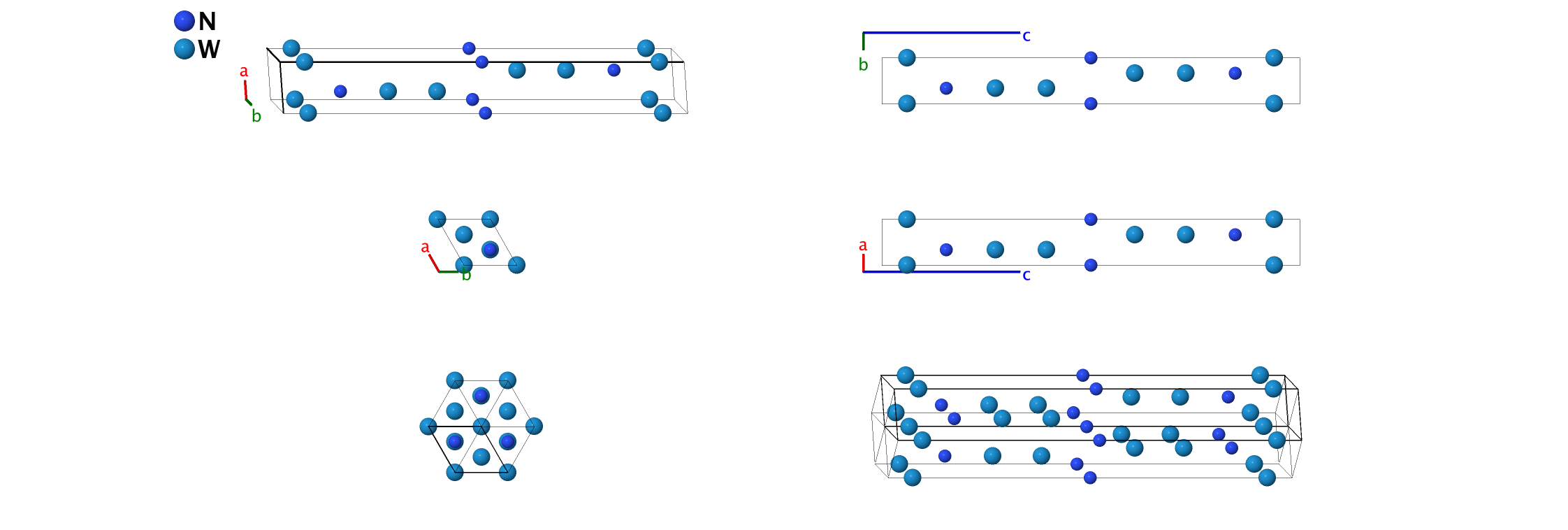
deltaHII–NW2 Structure: AB2_hP9_164_bd_c2d
| Prototype | : | HIINW2 |
| AFLOW prototype label | : | AB2_hP9_164_bd_c2d |
| Strukturbericht designation | : | None |
| Pearson symbol | : | hP9 |
| Space group number | : | 164 |
| Space group symbol | : | $P\bar{3}m1$ |
| AFLOW prototype command | : | aflow --proto=AB2_hP9_164_bd_c2d --params=$a,c/a,z_{2},z_{3},z_{4},z_{5}$ |
- Khitrova and Pinkser put this structure in space group P3 (#147), but the Wyckoff positions used are identical with space group P3m1 (#164), so we assign this to the higher symmetry space group.
Trigonal Hexagonal primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & \frac12 \, a \, \mathbf{\hat{x}} - \frac{\sqrt3}2 \, a \, \mathbf{\hat{y}} \\
\mathbf{a}_2 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac{\sqrt3}2 \, a \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \, \mathbf{\hat{z}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = & \frac{1}{2} \, \mathbf{a}_{3} & = & \frac{1}{2}c \, \mathbf{\hat{z}} & \left(1b\right) & \mbox{N I} \\ \mathbf{B}_{2} & = & z_{2} \, \mathbf{a}_{3} & = & z_{2}c \, \mathbf{\hat{z}} & \left(2c\right) & \mbox{W I} \\ \mathbf{B}_{3} & = & -z_{2} \, \mathbf{a}_{3} & = & -z_{2}c \, \mathbf{\hat{z}} & \left(2c\right) & \mbox{W I} \\ \mathbf{B}_{4} & = & \frac{1}{3} \, \mathbf{a}_{1} + \frac{2}{3} \, \mathbf{a}_{2} + z_{3} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{x}} + \frac{1}{2\sqrt{3}}a \, \mathbf{\hat{y}} + z_{3}c \, \mathbf{\hat{z}} & \left(2d\right) & \mbox{N II} \\ \mathbf{B}_{5} & = & \frac{2}{3} \, \mathbf{a}_{1} + \frac{1}{3} \, \mathbf{a}_{2}-z_{3} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{x}}- \frac{1}{2\sqrt{3}}a \, \mathbf{\hat{y}}-z_{3}c \, \mathbf{\hat{z}} & \left(2d\right) & \mbox{N II} \\ \mathbf{B}_{6} & = & \frac{1}{3} \, \mathbf{a}_{1} + \frac{2}{3} \, \mathbf{a}_{2} + z_{4} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{x}} + \frac{1}{2\sqrt{3}}a \, \mathbf{\hat{y}} + z_{4}c \, \mathbf{\hat{z}} & \left(2d\right) & \mbox{W II} \\ \mathbf{B}_{7} & = & \frac{2}{3} \, \mathbf{a}_{1} + \frac{1}{3} \, \mathbf{a}_{2}-z_{4} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{x}}- \frac{1}{2\sqrt{3}}a \, \mathbf{\hat{y}}-z_{4}c \, \mathbf{\hat{z}} & \left(2d\right) & \mbox{W II} \\ \mathbf{B}_{8} & = & \frac{1}{3} \, \mathbf{a}_{1} + \frac{2}{3} \, \mathbf{a}_{2} + z_{5} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{x}} + \frac{1}{2\sqrt{3}}a \, \mathbf{\hat{y}} + z_{5}c \, \mathbf{\hat{z}} & \left(2d\right) & \mbox{W III} \\ \mathbf{B}_{9} & = & \frac{2}{3} \, \mathbf{a}_{1} + \frac{1}{3} \, \mathbf{a}_{2}-z_{5} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{x}}- \frac{1}{2\sqrt{3}}a \, \mathbf{\hat{y}}-z_{5}c \, \mathbf{\hat{z}} & \left(2d\right) & \mbox{W III} \\ \end{array} \]References
- V. I. Khitrova and Z. G. Pinkser, Chemical Crystallography of Tungsten Nitrides and of Some Other Interstitial Phases, Sov. Phys. Crystallogr. 6, 712–719 (1961).