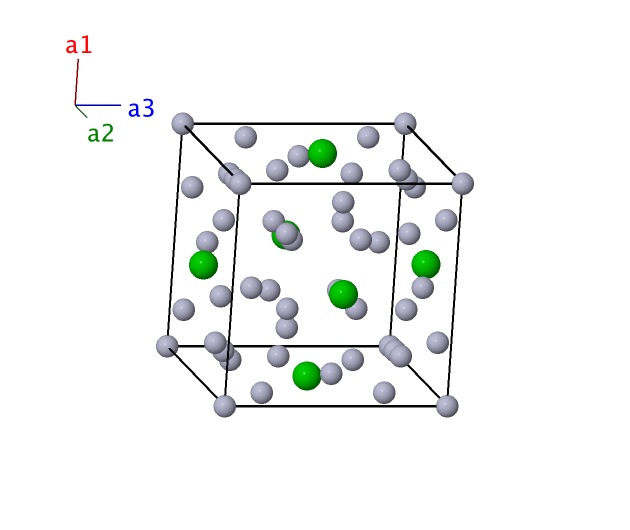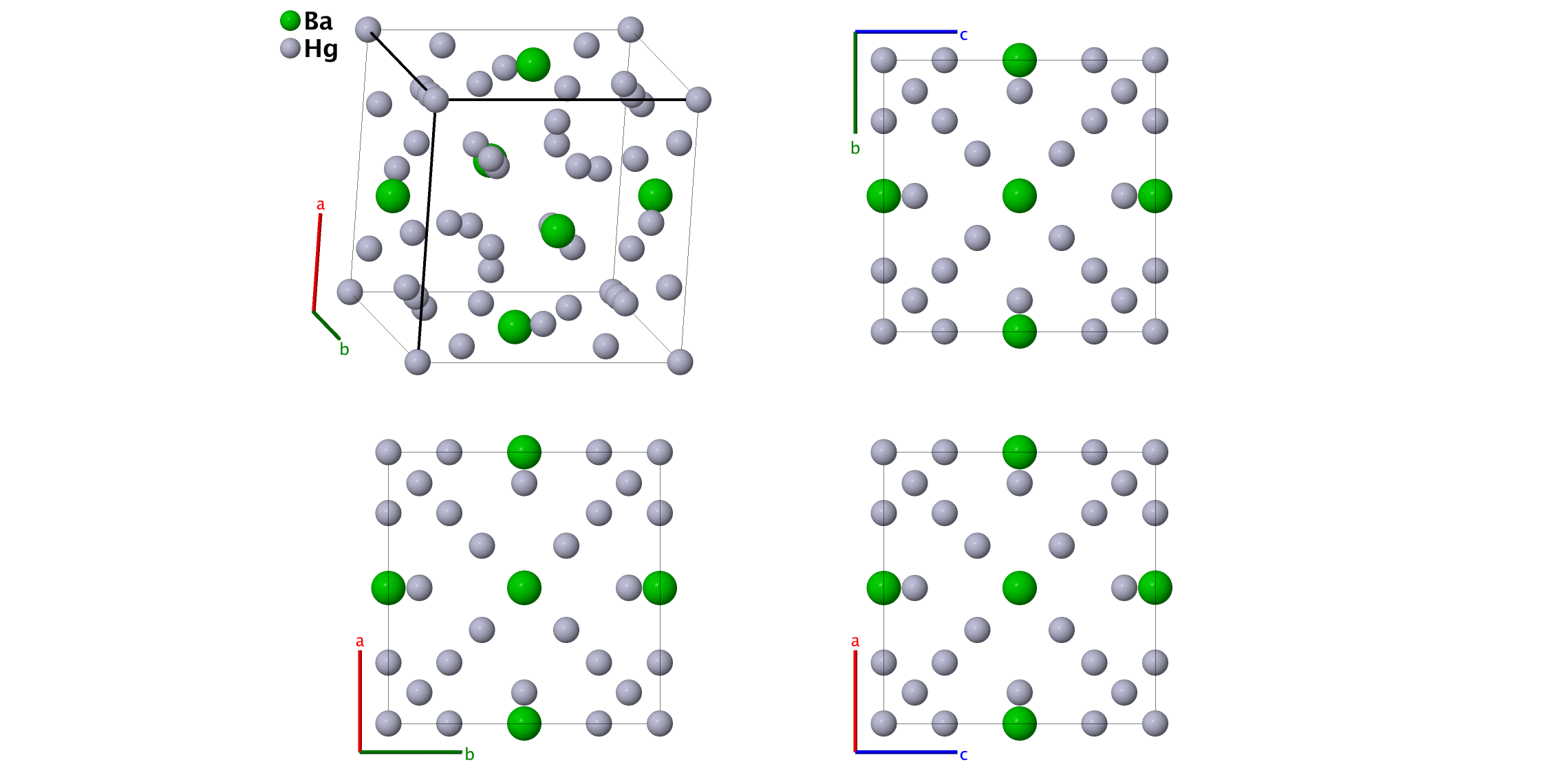
BaHg11 (D2e) Structure: AB11_cP36_221_c_agij
| Prototype | : | BaHg11 |
| AFLOW prototype label | : | AB11_cP36_221_c_agij |
| Strukturbericht designation | : | $D2_{e}$ |
| Pearson symbol | : | cP36 |
| Space group number | : | 221 |
| Space group symbol | : | $\mbox{Pm}\bar{3}\mbox{m}$ |
| AFLOW prototype command | : | aflow --proto=AB11_cP36_221_c_agij --params=$a,x_{3},y_{4},y_{5}$ |
Other compounds with this structure
A number of Hg and Cd phases with Group I or IIA metals or rare earths.
(Pearson, 1972) pp. 751–752.
Simple Cubic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \\
\mathbf{a}_2 & = & a \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & a \, \mathbf{\hat{z}}
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = &0 \, \mathbf{a}_{1} + 0 \, \mathbf{a}_{2} + 0 \, \mathbf{a}_{3} & = &0 \mathbf{\hat{x}} + 0 \mathbf{\hat{y}} + 0 \mathbf{\hat{z}} & \left(1a\right) & \mbox{Hg I} \\ \mathbf{B}_{2} & = &\frac12 \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\hat{y}}+ \frac12 \, a \, \mathbf{\hat{z}}& \left(3c\right) & \mbox{Ba} \\ \mathbf{B}_{3} & = &\frac12 \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\hat{x}}+ \frac12 \, a \, \mathbf{\hat{z}}& \left(3c\right) & \mbox{Ba} \\ \mathbf{B}_{4} & = &\frac12 \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{2}& = &\frac12 \, a \, \mathbf{\hat{x}}+ \frac12 \, a \, \mathbf{\hat{y}}& \left(3c\right) & \mbox{Ba} \\ \mathbf{B}_{5} & = &x_{3} \, \mathbf{a}_{1}+ x_{3} \, \mathbf{a}_{2}+ x_{3} \, \mathbf{a}_{3}& = &x_{3} \, a \, \mathbf{\hat{x}}+ x_{3} \, a \, \mathbf{\hat{y}}+ x_{3} \, a \, \mathbf{\hat{z}}& \left(8g\right) & \mbox{Hg II} \\ \mathbf{B}_{6} & = &- x_{3} \, \mathbf{a}_{1}- x_{3} \, \mathbf{a}_{2}+ x_{3} \, \mathbf{a}_{3}& = &- x_{3} \, a \, \mathbf{\hat{x}}- x_{3} \, a \, \mathbf{\hat{y}}+ x_{3} \, a \, \mathbf{\hat{z}}& \left(8g\right) & \mbox{Hg II} \\ \mathbf{B}_{7} & = &- x_{3} \, \mathbf{a}_{1}+ x_{3} \, \mathbf{a}_{2}- x_{3} \, \mathbf{a}_{3}& = &- x_{3} \, a \, \mathbf{\hat{x}}+ x_{3} \, a \, \mathbf{\hat{y}}- x_{3} \, a \, \mathbf{\hat{z}}& \left(8g\right) & \mbox{Hg II} \\ \mathbf{B}_{8} & = &x_{3} \, \mathbf{a}_{1}- x_{3} \, \mathbf{a}_{2}- x_{3} \, \mathbf{a}_{3}& = &x_{3} \, a \, \mathbf{\hat{x}}- x_{3} \, a \, \mathbf{\hat{y}}- x_{3} \, a \, \mathbf{\hat{z}}& \left(8g\right) & \mbox{Hg II} \\ \mathbf{B}_{9} & = &x_{3} \, \mathbf{a}_{1}+ x_{3} \, \mathbf{a}_{2}- x_{3} \, \mathbf{a}_{3}& = &x_{3} \, a \, \mathbf{\hat{x}}+ x_{3} \, a \, \mathbf{\hat{y}}- x_{3} \, a \, \mathbf{\hat{z}}& \left(8g\right) & \mbox{Hg II} \\ \mathbf{B}_{10} & = &- x_{3} \, \mathbf{a}_{1}- x_{3} \, \mathbf{a}_{2}- x_{3} \, \mathbf{a}_{3}& = &- x_{3} \, a \, \mathbf{\hat{x}}- x_{3} \, a \, \mathbf{\hat{y}}- x_{3} \, a \, \mathbf{\hat{z}}& \left(8g\right) & \mbox{Hg II} \\ \mathbf{B}_{11} & = &x_{3} \, \mathbf{a}_{1}- x_{3} \, \mathbf{a}_{2}+ x_{3} \, \mathbf{a}_{3}& = &x_{3} \, a \, \mathbf{\hat{x}}- x_{3} \, a \, \mathbf{\hat{y}}+ x_{3} \, a \, \mathbf{\hat{z}}& \left(8g\right) & \mbox{Hg II} \\ \mathbf{B}_{12} & = &- x_{3} \, \mathbf{a}_{1}+ x_{3} \, \mathbf{a}_{2}+ x_{3} \, \mathbf{a}_{3}& = &- x_{3} \, a \, \mathbf{\hat{x}}+ x_{3} \, a \, \mathbf{\hat{y}}+ x_{3} \, a \, \mathbf{\hat{z}}& \left(8g\right) & \mbox{Hg II} \\ \mathbf{B}_{13} & = &y_{4} \, \mathbf{a}_{2}+ y_{4} \, \mathbf{a}_{3}& = &y_{4} \, a \, \mathbf{\hat{y}}+ y_{4} \, a \, \mathbf{\hat{z}}& \left(12i\right) & \mbox{Hg III} \\ \mathbf{B}_{14} & = &y_{4} \, \mathbf{a}_{2}- y_{4} \, \mathbf{a}_{3}& = &y_{4} \, a \, \mathbf{\hat{y}}- y_{4} \, a \, \mathbf{\hat{z}}& \left(12i\right) & \mbox{Hg III} \\ \mathbf{B}_{15} & = &- y_{4} \, \mathbf{a}_{2}+ y_{4} \, \mathbf{a}_{3}& = &- y_{4} \, a \, \mathbf{\hat{y}}+ y_{4} \, a \, \mathbf{\hat{z}}& \left(12i\right) & \mbox{Hg III} \\ \mathbf{B}_{16} & = &- y_{4} \, \mathbf{a}_{2}- y_{4} \, \mathbf{a}_{3}& = &- y_{4} \, a \, \mathbf{\hat{y}}- y_{4} \, a \, \mathbf{\hat{z}}& \left(12i\right) & \mbox{Hg III} \\ \mathbf{B}_{17} & = &y_{4} \, \mathbf{a}_{1}+ y_{4} \, \mathbf{a}_{3}& = &y_{4} \, a \, \mathbf{\hat{x}}+ y_{4} \, a \, \mathbf{\hat{z}}& \left(12i\right) & \mbox{Hg III} \\ \mathbf{B}_{18} & = &y_{4} \, \mathbf{a}_{1}- y_{4} \, \mathbf{a}_{3}& = &y_{4} \, a \, \mathbf{\hat{x}}- y_{4} \, a \, \mathbf{\hat{z}}& \left(12i\right) & \mbox{Hg III} \\ \mathbf{B}_{19} & = &- y_{4} \, \mathbf{a}_{1}+ y_{4} \, \mathbf{a}_{3}& = &- y_{4} \, a \, \mathbf{\hat{x}}+ y_{4} \, a \, \mathbf{\hat{z}}& \left(12i\right) & \mbox{Hg III} \\ \mathbf{B}_{20} & = &- y_{4} \, \mathbf{a}_{1}- y_{4} \, \mathbf{a}_{3}& = &- y_{4} \, a \, \mathbf{\hat{x}}- y_{4} \, a \, \mathbf{\hat{z}}& \left(12i\right) & \mbox{Hg III} \\ \mathbf{B}_{21} & = &y_{4} \, \mathbf{a}_{1}+ y_{4} \, \mathbf{a}_{2}& = &y_{4} \, a \, \mathbf{\hat{x}}+ y_{4} \, a \, \mathbf{\hat{y}}& \left(12i\right) & \mbox{Hg III} \\ \mathbf{B}_{22} & = &y_{4} \, \mathbf{a}_{1}- y_{4} \, \mathbf{a}_{2}& = &y_{4} \, a \, \mathbf{\hat{x}}- y_{4} \, a \, \mathbf{\hat{y}}& \left(12i\right) & \mbox{Hg III} \\ \mathbf{B}_{23} & = &- y_{4} \, \mathbf{a}_{1}+ y_{4} \, \mathbf{a}_{2}& = &- y_{4} \, a \, \mathbf{\hat{x}}+ y_{4} \, a \, \mathbf{\hat{y}}& \left(12i\right) & \mbox{Hg III} \\ \mathbf{B}_{24} & = &- y_{4} \, \mathbf{a}_{1}- y_{4} \, \mathbf{a}_{2}& = &- y_{4} \, a \, \mathbf{\hat{x}}- y_{4} \, a \, \mathbf{\hat{y}}& \left(12i\right) & \mbox{Hg III} \\ \mathbf{B}_{25} & = &\frac12 \, \mathbf{a}_{1}+ y_{5} \, \mathbf{a}_{2}+ y_{5} \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\hat{x}}+ y_{5} \, a \, \mathbf{\hat{y}}+ y_{5} \, a \, \mathbf{\hat{z}}& \left(12j\right) & \mbox{Hg IV} \\ \mathbf{B}_{26} & = &\frac12 \, \mathbf{a}_{1}+ y_{5} \, \mathbf{a}_{2}- y_{5} \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\hat{x}}+ y_{5} \, a \, \mathbf{\hat{y}}- y_{5} \, a \, \mathbf{\hat{z}}& \left(12j\right) & \mbox{Hg IV} \\ \mathbf{B}_{27} & = &\frac12 \, \mathbf{a}_{1}- y_{5} \, \mathbf{a}_{2}+ y_{5} \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\hat{x}}- y_{5} \, a \, \mathbf{\hat{y}}+ y_{5} \, a \, \mathbf{\hat{z}}& \left(12j\right) & \mbox{Hg IV} \\ \mathbf{B}_{28} & = &\frac12 \, \mathbf{a}_{1}- y_{5} \, \mathbf{a}_{2}- y_{5} \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\hat{x}}- y_{5} \, a \, \mathbf{\hat{y}}- y_{5} \, a \, \mathbf{\hat{z}}& \left(12j\right) & \mbox{Hg IV} \\ \mathbf{B}_{29} & = &y_{5} \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{2}+ y_{5} \, \mathbf{a}_{3}& = &y_{5} \, a \, \mathbf{\hat{x}}+ \frac12 \, a \, \mathbf{\hat{y}}+ y_{5} \, a \, \mathbf{\hat{z}}& \left(12j\right) & \mbox{Hg IV} \\ \mathbf{B}_{30} & = &y_{5} \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{2}- y_{5} \, \mathbf{a}_{3}& = &y_{5} \, a \, \mathbf{\hat{x}}+ \frac12 \, a \, \mathbf{\hat{y}}- y_{5} \, a \, \mathbf{\hat{z}}& \left(12j\right) & \mbox{Hg IV} \\ \mathbf{B}_{31} & = &- y_{5} \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{2}+ y_{5} \, \mathbf{a}_{3}& = &- y_{5} \, a \, \mathbf{\hat{x}}+ \frac12 \, a \, \mathbf{\hat{y}}+ y_{5} \, a \, \mathbf{\hat{z}}& \left(12j\right) & \mbox{Hg IV} \\ \mathbf{B}_{32} & = &- y_{5} \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{2}- y_{5} \, \mathbf{a}_{3}& = &- y_{5} \, a \, \mathbf{\hat{x}}+ \frac12 \, a \, \mathbf{\hat{y}}- y_{5} \, a \, \mathbf{\hat{z}}& \left(12j\right) & \mbox{Hg IV} \\ \mathbf{B}_{33} & = &y_{5} \, \mathbf{a}_{1}+ y_{5} \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& = &y_{5} \, a \, \mathbf{\hat{x}}+ y_{5} \, a \, \mathbf{\hat{y}}+ \frac12 \, a \, \mathbf{\hat{z}}& \left(12j\right) & \mbox{Hg IV} \\ \mathbf{B}_{34} & = &y_{5} \, \mathbf{a}_{1}- y_{5} \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& = &y_{5} \, a \, \mathbf{\hat{x}}- y_{5} \, a \, \mathbf{\hat{y}}+ \frac12 \, a \, \mathbf{\hat{z}}& \left(12j\right) & \mbox{Hg IV} \\ \mathbf{B}_{35} & = &- y_{5} \, \mathbf{a}_{1}+ y_{5} \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& = &- y_{5} \, a \, \mathbf{\hat{x}}+ y_{5} \, a \, \mathbf{\hat{y}}+ \frac12 \, a \, \mathbf{\hat{z}}& \left(12j\right) & \mbox{Hg IV} \\ \mathbf{B}_{36} & = &- y_{5} \, \mathbf{a}_{1}- y_{5} \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& = &- y_{5} \, a \, \mathbf{\hat{x}}- y_{5} \, a \, \mathbf{\hat{y}}+ \frac12 \, a \, \mathbf{\hat{z}}& \left(12j\right) & \mbox{Hg IV} \\ \end{array} \]References
- G. Peyronel, Struttura della fase BaHg11, Gazz. Chim. Ital. 82, 679–690 (1952).
Found in
- P. Villars, Material Phases Data System ((MPDS), CH–6354 Vitznau, Switzerland, 2014). Accessed through the Springer Materials site.