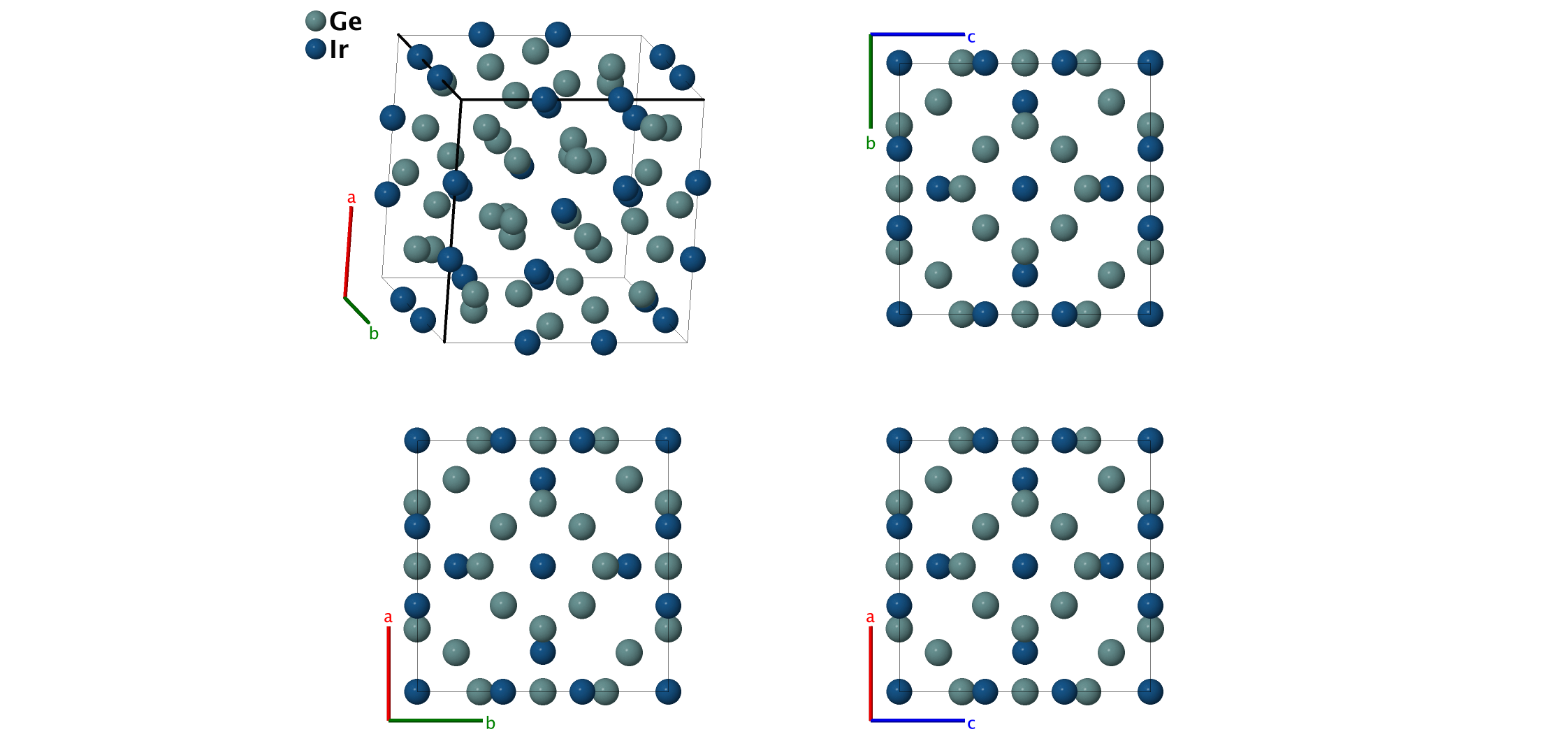
Ir3Ge7 ($D8_{f}$) Structure: A7B3_cI40_229_df_e
| Prototype | : | Ir3Ge7 |
| AFLOW prototype label | : | A7B3_cI40_229_df_e |
| Strukturbericht designation | : | $D8_{f}$ |
| Pearson symbol | : | cI40 |
| Space group number | : | 229 |
| Space group symbol | : | $Im\bar{3}m$ |
| AFLOW prototype command | : | aflow --proto=A7B3_cI40_229_df_e --params=$a,x_{2},x_{3}$ |
Other compounds with this structure
- Ga7Ni3, In7Pd3, Sb7Mo3, As7Re3, Sn7Ru3
Body-centered Cubic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & - \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, a \, \mathbf{\hat{y}} + \frac12 \, a \, \mathbf{\hat{z}} \\
\mathbf{a}_2 & = & ~ \frac12 \, a \, \mathbf{\hat{x}} - \frac12 \, a \, \mathbf{\hat{y}} + \frac12 \, a \, \mathbf{\hat{z}} \\
\mathbf{a}_3 & = & ~ \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, a \, \mathbf{\hat{y}} - \frac12 \, a \, \mathbf{\hat{z}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = & \frac{1}{2} \, \mathbf{a}_{1} + \frac{3}{4} \, \mathbf{a}_{2} + \frac{1}{4} \, \mathbf{a}_{3} & = & \frac{1}{4}a \, \mathbf{\hat{x}} + \frac{1}{2}a \, \mathbf{\hat{z}} & \left(12d\right) & \mbox{Ge I} \\ \mathbf{B}_{2} & = & \frac{1}{2} \, \mathbf{a}_{1} + \frac{1}{4} \, \mathbf{a}_{2} + \frac{3}{4} \, \mathbf{a}_{3} & = & \frac{1}{4}a \, \mathbf{\hat{x}} + \frac{1}{2}a \, \mathbf{\hat{y}} & \left(12d\right) & \mbox{Ge I} \\ \mathbf{B}_{3} & = & \frac{1}{4} \, \mathbf{a}_{1} + \frac{1}{2} \, \mathbf{a}_{2} + \frac{3}{4} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{x}} + \frac{1}{4}a \, \mathbf{\hat{y}} & \left(12d\right) & \mbox{Ge I} \\ \mathbf{B}_{4} & = & \frac{3}{4} \, \mathbf{a}_{1} + \frac{1}{2} \, \mathbf{a}_{2} + \frac{1}{4} \, \mathbf{a}_{3} & = & \frac{1}{4}a \, \mathbf{\hat{y}} + \frac{1}{2}a \, \mathbf{\hat{z}} & \left(12d\right) & \mbox{Ge I} \\ \mathbf{B}_{5} & = & \frac{3}{4} \, \mathbf{a}_{1} + \frac{1}{4} \, \mathbf{a}_{2} + \frac{1}{2} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{y}} + \frac{1}{4}a \, \mathbf{\hat{z}} & \left(12d\right) & \mbox{Ge I} \\ \mathbf{B}_{6} & = & \frac{1}{4} \, \mathbf{a}_{1} + \frac{3}{4} \, \mathbf{a}_{2} + \frac{1}{2} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{x}} + \frac{1}{4}a \, \mathbf{\hat{z}} & \left(12d\right) & \mbox{Ge I} \\ \mathbf{B}_{7} & = & x_{2} \, \mathbf{a}_{2} + x_{2} \, \mathbf{a}_{3} & = & x_{2}a \, \mathbf{\hat{x}} & \left(12e\right) & \mbox{Ir} \\ \mathbf{B}_{8} & = & -x_{2} \, \mathbf{a}_{2}-x_{2} \, \mathbf{a}_{3} & = & -x_{2}a \, \mathbf{\hat{x}} & \left(12e\right) & \mbox{Ir} \\ \mathbf{B}_{9} & = & x_{2} \, \mathbf{a}_{1} + x_{2} \, \mathbf{a}_{3} & = & x_{2}a \, \mathbf{\hat{y}} & \left(12e\right) & \mbox{Ir} \\ \mathbf{B}_{10} & = & -x_{2} \, \mathbf{a}_{1}-x_{2} \, \mathbf{a}_{3} & = & -x_{2}a \, \mathbf{\hat{y}} & \left(12e\right) & \mbox{Ir} \\ \mathbf{B}_{11} & = & x_{2} \, \mathbf{a}_{1} + x_{2} \, \mathbf{a}_{2} & = & x_{2}a \, \mathbf{\hat{z}} & \left(12e\right) & \mbox{Ir} \\ \mathbf{B}_{12} & = & -x_{2} \, \mathbf{a}_{1}-x_{2} \, \mathbf{a}_{2} & = & -x_{2}a \, \mathbf{\hat{z}} & \left(12e\right) & \mbox{Ir} \\ \mathbf{B}_{13} & = & 2x_{3} \, \mathbf{a}_{1} + 2x_{3} \, \mathbf{a}_{2} + 2x_{3} \, \mathbf{a}_{3} & = & x_{3}a \, \mathbf{\hat{x}} + x_{3}a \, \mathbf{\hat{y}} + x_{3}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Ge II} \\ \mathbf{B}_{14} & = & -2x_{3} \, \mathbf{a}_{3} & = & -x_{3}a \, \mathbf{\hat{x}}-x_{3}a \, \mathbf{\hat{y}} + x_{3}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Ge II} \\ \mathbf{B}_{15} & = & -2x_{3} \, \mathbf{a}_{2} & = & -x_{3}a \, \mathbf{\hat{x}} + x_{3}a \, \mathbf{\hat{y}}-x_{3}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Ge II} \\ \mathbf{B}_{16} & = & -2x_{3} \, \mathbf{a}_{1} & = & x_{3}a \, \mathbf{\hat{x}}-x_{3}a \, \mathbf{\hat{y}}-x_{3}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Ge II} \\ \mathbf{B}_{17} & = & 2x_{3} \, \mathbf{a}_{3} & = & x_{3}a \, \mathbf{\hat{x}} + x_{3}a \, \mathbf{\hat{y}}-x_{3}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Ge II} \\ \mathbf{B}_{18} & = & -2x_{3} \, \mathbf{a}_{1}-2x_{3} \, \mathbf{a}_{2}-2x_{3} \, \mathbf{a}_{3} & = & -x_{3}a \, \mathbf{\hat{x}}-x_{3}a \, \mathbf{\hat{y}}-x_{3}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Ge II} \\ \mathbf{B}_{19} & = & 2x_{3} \, \mathbf{a}_{2} & = & x_{3}a \, \mathbf{\hat{x}}-x_{3}a \, \mathbf{\hat{y}} + x_{3}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Ge II} \\ \mathbf{B}_{20} & = & 2x_{3} \, \mathbf{a}_{1} & = & -x_{3}a \, \mathbf{\hat{x}} + x_{3}a \, \mathbf{\hat{y}} + x_{3}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Ge II} \\ \end{array} \]References
- U. Häussermann, M. Elding–Pontén, C. Svensson, and S. Lidin, Compounds with the Ir3Ge7 Structure Type: Interpenetrating Frameworks with Flexible Bonding Properties, Chem. Eur. J. 4, 1007–1015 (1998), doi:10.1002/(SICI)1521-3765(19980615)4:6%3C1007::AID-CHEM1007%3E3.0.CO;2-7.
Found in
- F. Selim, J. P. Bevington, and G. S. Collins, Diffusion of 111Cd probes in Ga7Pt3 studied via nuclear quadrupole relaxation, Hyperfine Interact. 178, 87–90 (2007), doi:10.1007/s10751-008-9663-3.