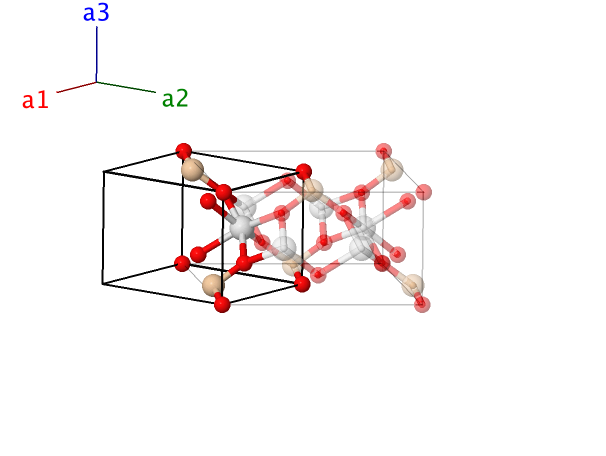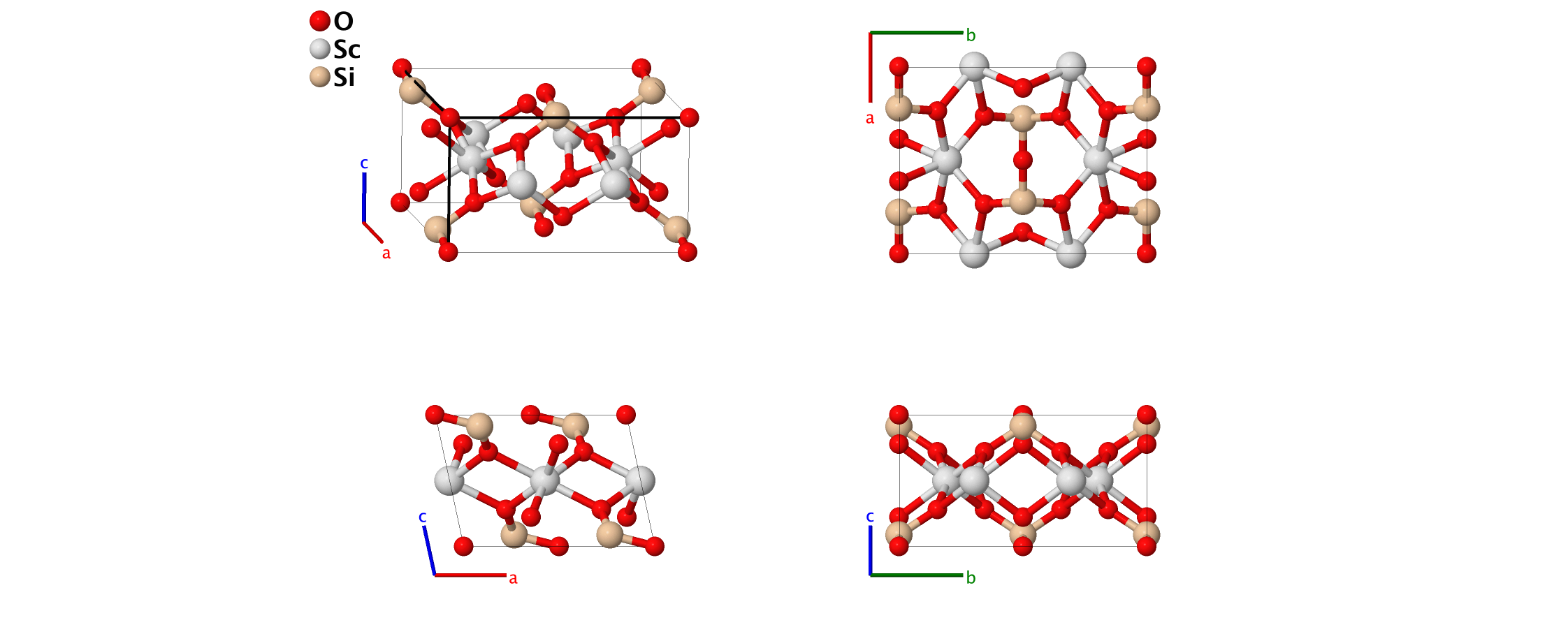
Thortveitite ([Sc,Y]2Si2O7, $S2_{1}$) Structure: A7B2C2_mC22_12_aij_h_i
| Prototype | : | [Sc,Y]2Si2O7 |
| AFLOW prototype label | : | A7B2C2_mC22_12_aij_h_i |
| Strukturbericht designation | : | $S2_{1}$ |
| Pearson symbol | : | mC22 |
| Space group number | : | 12 |
| Space group symbol | : | $C2/m$ |
| AFLOW prototype command | : | aflow --proto=A7B2C2_mC22_12_aij_h_i --params=$a,b/a,c/a,\beta,y_{2},x_{3},z_{3},x_{4},z_{4},x_{5},y_{5},z_{5}$ |
Other compounds with this structure
- $\beta$-Er2Si2O7, $\beta$-Ho2Si2O7, $\beta$-In2Si2O7, $\beta$-Lu2Si2O7, $\beta$-Sc2Si2O7, $\beta$-Tm2Si2O7, $\beta$-Y2Si2O7, $\beta$-Yb2Si2O7, $\beta$-[Y,Sc]2Si2O7, and $\beta$-[Y,Yb]2Si2O7
- Thortveitite is the primary source of scandium, and is one of the simplest sorosilicates, i.e., minerals with isolated Si2O7 groups (Bianchi, 1988). Although the (4h) Wyckoff position is randomly occupied by both Sc and Y atoms, we use Sc to represent the site. (Bianchi, 1988) gives structural information for several samples of thortveitite. We use the data from sample 1, collected in Iveland, Norway.
Base-centered Monoclinic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & \frac12 \, a \, \mathbf{\hat{x}} - \frac12 \, b \, \mathbf{\hat{y}} \\
\mathbf{a}_2 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, b \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \cos\beta \, \mathbf{\hat{x}} + c \sin\beta \, \mathbf{\hat{z}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = & 0 \, \mathbf{a}_{1} + 0 \, \mathbf{a}_{2} + 0 \, \mathbf{a}_{3} & = & 0 \, \mathbf{\hat{x}} + 0 \, \mathbf{\hat{y}} + 0 \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{O I} \\ \mathbf{B}_{2} & = & -y_{2} \, \mathbf{a}_{1} + y_{2} \, \mathbf{a}_{2} + \frac{1}{2} \, \mathbf{a}_{3} & = & \frac{1}{2}c\cos\beta \, \mathbf{\hat{x}} + y_{2}b \, \mathbf{\hat{y}} + \frac{1}{2}c\sin\beta \, \mathbf{\hat{z}} & \left(4h\right) & \mbox{Sc} \\ \mathbf{B}_{3} & = & y_{2} \, \mathbf{a}_{1}-y_{2} \, \mathbf{a}_{2} + \frac{1}{2} \, \mathbf{a}_{3} & = & \frac{1}{2}c\cos\beta \, \mathbf{\hat{x}}-y_{2}b \, \mathbf{\hat{y}} + \frac{1}{2}c\sin\beta \, \mathbf{\hat{z}} & \left(4h\right) & \mbox{Sc} \\ \mathbf{B}_{4} & = & x_{3} \, \mathbf{a}_{1} + x_{3} \, \mathbf{a}_{2} + z_{3} \, \mathbf{a}_{3} & = & \left(x_{3}a+z_{3}c\cos\beta\right) \, \mathbf{\hat{x}} + z_{3}c\sin\beta \, \mathbf{\hat{z}} & \left(4i\right) & \mbox{O II} \\ \mathbf{B}_{5} & = & -x_{3} \, \mathbf{a}_{1}-x_{3} \, \mathbf{a}_{2}-z_{3} \, \mathbf{a}_{3} & = & \left(-x_{3}a-z_{3}c\cos\beta\right) \, \mathbf{\hat{x}}-z_{3}c\sin\beta \, \mathbf{\hat{z}} & \left(4i\right) & \mbox{O II} \\ \mathbf{B}_{6} & = & x_{4} \, \mathbf{a}_{1} + x_{4} \, \mathbf{a}_{2} + z_{4} \, \mathbf{a}_{3} & = & \left(x_{4}a+z_{4}c\cos\beta\right) \, \mathbf{\hat{x}} + z_{4}c\sin\beta \, \mathbf{\hat{z}} & \left(4i\right) & \mbox{Si} \\ \mathbf{B}_{7} & = & -x_{4} \, \mathbf{a}_{1}-x_{4} \, \mathbf{a}_{2}-z_{4} \, \mathbf{a}_{3} & = & \left(-x_{4}a-z_{4}c\cos\beta\right) \, \mathbf{\hat{x}}-z_{4}c\sin\beta \, \mathbf{\hat{z}} & \left(4i\right) & \mbox{Si} \\ \mathbf{B}_{8} & = & \left(x_{5}-y_{5}\right) \, \mathbf{a}_{1} + \left(x_{5}+y_{5}\right) \, \mathbf{a}_{2} + z_{5} \, \mathbf{a}_{3} & = & \left(x_{5}a+z_{5}c\cos\beta\right) \, \mathbf{\hat{x}} + y_{5}b \, \mathbf{\hat{y}} + z_{5}c\sin\beta \, \mathbf{\hat{z}} & \left(8j\right) & \mbox{O III} \\ \mathbf{B}_{9} & = & \left(-x_{5}-y_{5}\right) \, \mathbf{a}_{1} + \left(-x_{5}+y_{5}\right) \, \mathbf{a}_{2}-z_{5} \, \mathbf{a}_{3} & = & \left(-x_{5}a-z_{5}c\cos\beta\right) \, \mathbf{\hat{x}} + y_{5}b \, \mathbf{\hat{y}}-z_{5}c\sin\beta \, \mathbf{\hat{z}} & \left(8j\right) & \mbox{O III} \\ \mathbf{B}_{10} & = & \left(-x_{5}+y_{5}\right) \, \mathbf{a}_{1} + \left(-x_{5}-y_{5}\right) \, \mathbf{a}_{2}-z_{5} \, \mathbf{a}_{3} & = & \left(-x_{5}a-z_{5}c\cos\beta\right) \, \mathbf{\hat{x}}-y_{5}b \, \mathbf{\hat{y}}-z_{5}c\sin\beta \, \mathbf{\hat{z}} & \left(8j\right) & \mbox{O III} \\ \mathbf{B}_{11} & = & \left(x_{5}+y_{5}\right) \, \mathbf{a}_{1} + \left(x_{5}-y_{5}\right) \, \mathbf{a}_{2} + z_{5} \, \mathbf{a}_{3} & = & \left(x_{5}a+z_{5}c\cos\beta\right) \, \mathbf{\hat{x}}-y_{5}b \, \mathbf{\hat{y}} + z_{5}c\sin\beta \, \mathbf{\hat{z}} & \left(8j\right) & \mbox{O III} \\ \end{array} \]References
- R. Bianchi, T. Pilati, V. Diella, C. M. Gramaccioli, and G. Mannucci, A re–examination of thortveitite, Am. Mineral. 73, 601–607 (1988).
Found in
- R. T. Downs and M. Hall–Wallace, The American Mineralogist Crystal Structure Database, Am. Mineral. 88, 247–250 (2003).