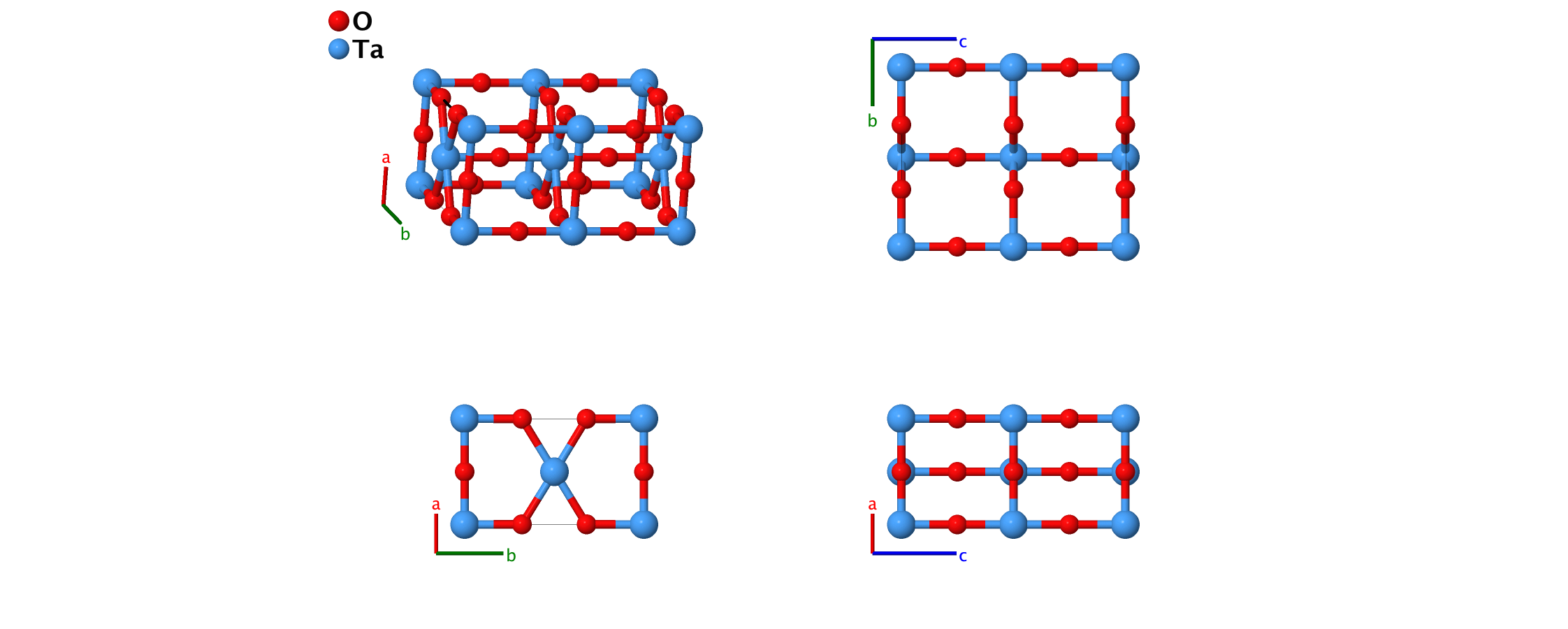
$\beta$–Ta2O5 Structure: A5B2_oP14_49_dehq_ab
| Prototype | : | Ta2O5 |
| AFLOW prototype label | : | A5B2_oP14_49_dehq_ab |
| Strukturbericht designation | : | None |
| Pearson symbol | : | oP14 |
| Space group number | : | 49 |
| Space group symbol | : | $Pccm$ |
| AFLOW prototype command | : | aflow --proto=A5B2_oP14_49_dehq_ab --params=$a,b/a,c/a,x_{6},y_{6}$ |
- While FINDSYM identifies space group #49 for this structure (consistent with the reference), AFLOW–SYM and Platon identify #47. Lowering the tolerance value for AFLOW–SYM resolves the expected space group #49. Space groups #47 and #49 are both reasonable classifications since they are commensurate with subgroup relations.
Simple Orthorhombic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \\
\mathbf{a}_2 & = & b \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \, \mathbf{\hat{z}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = & 0 \, \mathbf{a}_{1} + 0 \, \mathbf{a}_{2} + 0 \, \mathbf{a}_{3} & = & 0 \, \mathbf{\hat{x}} + 0 \, \mathbf{\hat{y}} + 0 \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{Ta I} \\ \mathbf{B}_{2} & = & \frac{1}{2} \, \mathbf{a}_{3} & = & \frac{1}{2}c \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{Ta I} \\ \mathbf{B}_{3} & = & \frac{1}{2} \, \mathbf{a}_{1} + \frac{1}{2} \, \mathbf{a}_{2} & = & \frac{1}{2}a \, \mathbf{\hat{x}} + \frac{1}{2}b \, \mathbf{\hat{y}} & \left(2b\right) & \mbox{Ta II} \\ \mathbf{B}_{4} & = & \frac{1}{2} \, \mathbf{a}_{1} + \frac{1}{2} \, \mathbf{a}_{2} + \frac{1}{2} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{x}} + \frac{1}{2}b \, \mathbf{\hat{y}} + \frac{1}{2}c \, \mathbf{\hat{z}} & \left(2b\right) & \mbox{Ta II} \\ \mathbf{B}_{5} & = & \frac{1}{2} \, \mathbf{a}_{1} & = & \frac{1}{2}a \, \mathbf{\hat{x}} & \left(2d\right) & \mbox{O I} \\ \mathbf{B}_{6} & = & \frac{1}{2} \, \mathbf{a}_{1} + \frac{1}{2} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{x}} + \frac{1}{2}c \, \mathbf{\hat{z}} & \left(2d\right) & \mbox{O I} \\ \mathbf{B}_{7} & = & \frac{1}{4} \, \mathbf{a}_{3} & = & \frac{1}{4}c \, \mathbf{\hat{z}} & \left(2e\right) & \mbox{O II} \\ \mathbf{B}_{8} & = & \frac{3}{4} \, \mathbf{a}_{3} & = & \frac{3}{4}c \, \mathbf{\hat{z}} & \left(2e\right) & \mbox{O II} \\ \mathbf{B}_{9} & = & \frac{1}{2} \, \mathbf{a}_{1} + \frac{1}{2} \, \mathbf{a}_{2} + \frac{1}{4} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{x}} + \frac{1}{2}b \, \mathbf{\hat{y}} + \frac{1}{4}c \, \mathbf{\hat{z}} & \left(2h\right) & \mbox{O III} \\ \mathbf{B}_{10} & = & \frac{1}{2} \, \mathbf{a}_{1} + \frac{1}{2} \, \mathbf{a}_{2} + \frac{3}{4} \, \mathbf{a}_{3} & = & \frac{1}{2}a \, \mathbf{\hat{x}} + \frac{1}{2}b \, \mathbf{\hat{y}} + \frac{3}{4}c \, \mathbf{\hat{z}} & \left(2h\right) & \mbox{O III} \\ \mathbf{B}_{11} & = & x_{6} \, \mathbf{a}_{1} + y_{6} \, \mathbf{a}_{2} & = & x_{6}a \, \mathbf{\hat{x}} + y_{6}b \, \mathbf{\hat{y}} & \left(4q\right) & \mbox{O IV} \\ \mathbf{B}_{12} & = & -x_{6} \, \mathbf{a}_{1}-y_{6} \, \mathbf{a}_{2} & = & -x_{6}a \, \mathbf{\hat{x}}-y_{6}b \, \mathbf{\hat{y}} & \left(4q\right) & \mbox{O IV} \\ \mathbf{B}_{13} & = & -x_{6} \, \mathbf{a}_{1} + y_{6} \, \mathbf{a}_{2} + \frac{1}{2} \, \mathbf{a}_{3} & = & -x_{6}a \, \mathbf{\hat{x}} + y_{6}b \, \mathbf{\hat{y}} + \frac{1}{2}c \, \mathbf{\hat{z}} & \left(4q\right) & \mbox{O IV} \\ \mathbf{B}_{14} & = & x_{6} \, \mathbf{a}_{1}-y_{6} \, \mathbf{a}_{2} + \frac{1}{2} \, \mathbf{a}_{3} & = & x_{6}a \, \mathbf{\hat{x}}-y_{6}b \, \mathbf{\hat{y}} + \frac{1}{2}c \, \mathbf{\hat{z}} & \left(4q\right) & \mbox{O IV} \\ \end{array} \]References
- L. A. Aleshina and S. V. Loginova, Rietveld analysis of X–ray diffraction pattern from β–Ta2O5 oxide, Crystallogr. Rep. 47, 415–419 (2002), doi:10.1134/1.1481927.
- H. T. Stokes and D. M. Hatch, FINDSYM: Program for identifying the space group symmetry of a crystal, J. Appl. Crystallogr. 38, 237–238 (2005), doi:10.1107/S0021889804031528.
- D. Hicks, C. Oses, E. Gossett, G. Gomez, R. H. Taylor, C. Toher, M. J. Mehl, O. Levy, and S. Curtarolo, it AFLOW–SYM: platform for the complete, automatic and self–consistent symmetry analysis of crystals, Acta Crystallogr. Sect. A 74, 184–203 (2018), doi:10.1107/S2053273318003066.
- A. L. Spek, Single–crystal structure validation with the program PLATON, J. Appl. Crystallogr. 36, 7–13 (2003), doi:10.1107/S0021889802022112.
Found in
- P. Villars and K. Cenzual, Pearson's Crystal Data – Crystal Structure Database for Inorganic Compounds, ASM International (2013).