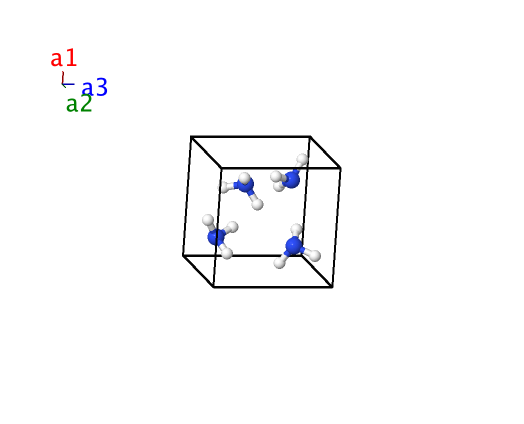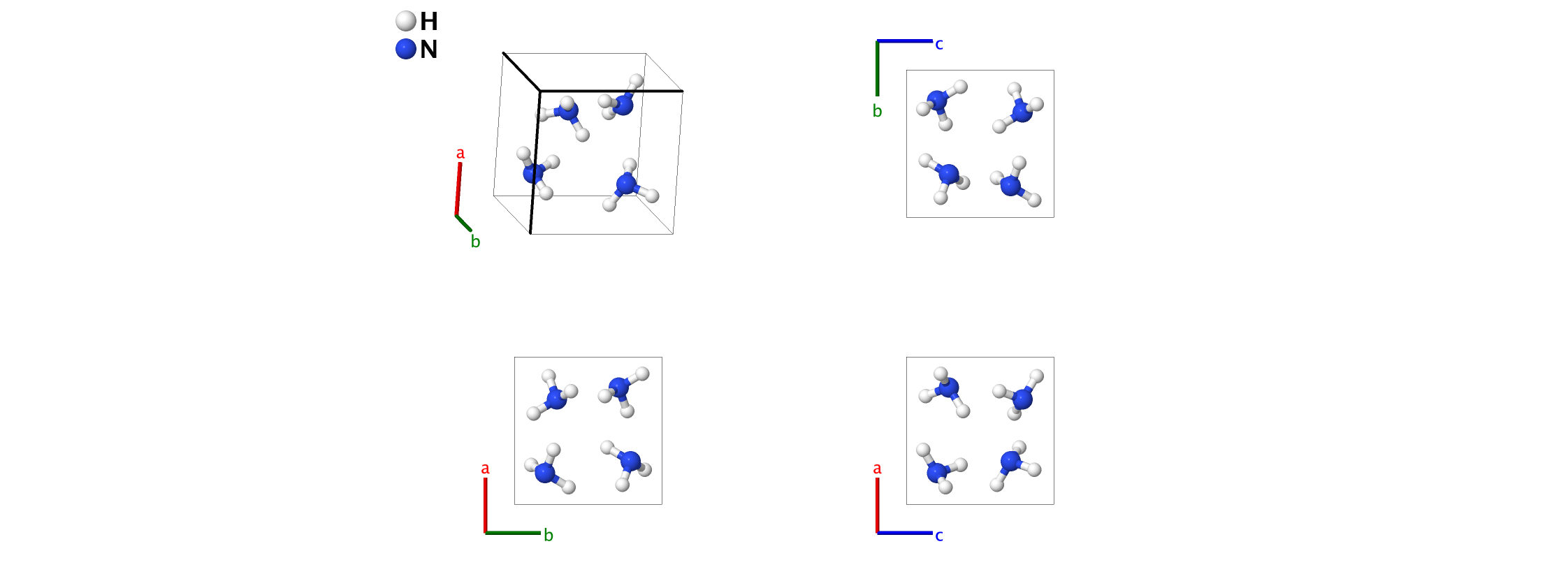
Ammonia (NH3, $D0_{1}$) Structure: A3B_cP16_198_b_a
| Prototype | : | NH3 |
| AFLOW prototype label | : | A3B_cP16_198_b_a |
| Strukturbericht designation | : | $D0_{1}$ |
| Pearson symbol | : | cP16 |
| Space group number | : | 198 |
| Space group symbol | : | $\mbox{P2}_{1}\mbox{3}$ |
| AFLOW prototype command | : | aflow --proto=A3B_cP16_198_b_a --params=$a,x_{1},x_{2},y_{2},z_{2}$ |
Other compounds with this structure
- AsH3, PH3
- The positions of the hydrogen atoms are taken from neutron diffraction data on fully deuterated ND3. In the original Strukturbericht (Ewald, 1931) gave this structure the symbol $D1$. Following the revision of the type-$D$ numbering beginning in volume II (Herman, 1937) this should be renamed $D0_{1}$. We previously used the $D1$ designation, but now list this as $D0_{1}$ for consistency with other $D$-type structures.
Simple Cubic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \\
\mathbf{a}_2 & = & a \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & a \, \mathbf{\hat{z}}
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = &x_{1} \, \mathbf{a}_{1}+ x_{1} \, \mathbf{a}_{2}+ x_{1} \, \mathbf{a}_{3}& = &x_{1} \, a \, \mathbf{\hat{x}}+ x_{1} \, a \, \mathbf{\hat{y}}+ x_{1} \, a \, \mathbf{\hat{z}}& \left(4a\right) & \mbox{N} \\ \mathbf{B}_{2} & = &\left(\frac12 - x_{1}\right) \, \mathbf{a}_{1}- x_{1} \, \mathbf{a}_{2}+ \left(\frac12 + x_{1}\right) \, \mathbf{a}_{3}& = &\left(\frac12 - x_{1}\right) \, a \, \mathbf{\hat{x}}- x_{1} \, a \, \mathbf{\hat{y}}+ \left(\frac12 + x_{1}\right) \, a \, \mathbf{\hat{z}}& \left(4a\right) & \mbox{N} \\ \mathbf{B}_{3} & = &- x_{1} \, \mathbf{a}_{1}+ \left(\frac12 + x_{1}\right) \, \mathbf{a}_{2}+ \left(\frac12 - x_{1}\right) \, \mathbf{a}_{3}& = &- x_{1} \, a \, \mathbf{\hat{x}}+ \left(\frac12 + x_{1}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac12 - x_{1}\right) \, a \, \mathbf{\hat{z}}& \left(4a\right) & \mbox{N} \\ \mathbf{B}_{4} & = &+ \left(\frac12 + x_{1}\right) \, \mathbf{a}_{1}+ \left(\frac12 - x_{1}\right) \, \mathbf{a}_{2}- x_{1} \, \mathbf{a}_{3}& = &+ \left(\frac12 + x_{1}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - x_{1}\right) \, a \, \mathbf{\hat{y}}- x_{1} \, a \, \mathbf{\hat{z}}& \left(4a\right) & \mbox{N} \\ \mathbf{B}_{5} & = &x_{2} \, \mathbf{a}_{1}+ y_{2} \, \mathbf{a}_{2}+ z_{2} \, \mathbf{a}_{3}& = &x_{2} \, a \, \mathbf{\hat{x}}+ y_{2} \, a \, \mathbf{\hat{y}}+ z_{2} \, a \, \mathbf{\hat{z}}& \left(12b\right) & \mbox{H} \\ \mathbf{B}_{6} & = &\left(\frac12 - x_{2}\right) \, \mathbf{a}_{1}- y_{2} \, \mathbf{a}_{2}+ \left(\frac12 + z_{2}\right) \, \mathbf{a}_{3}& = &\left(\frac12 - x_{2}\right) \, a \, \mathbf{\hat{x}}- y_{2} \, a \, \mathbf{\hat{y}}+ \left(\frac12 + z_{2}\right) \, a \, \mathbf{\hat{z}}& \left(12b\right) & \mbox{H} \\ \mathbf{B}_{7} & = &- x_{2} \, \mathbf{a}_{1}+ \left(\frac12 + y_{2}\right) \, \mathbf{a}_{2}+ \left(\frac12 - z_{2}\right) \, \mathbf{a}_{3}& = &- x_{2} \, a \, \mathbf{\hat{x}}+ \left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac12 - z_{2}\right) \, a \, \mathbf{\hat{z}}& \left(12b\right) & \mbox{H} \\ \mathbf{B}_{8} & = &+ \left(\frac12 + x_{2}\right) \, \mathbf{a}_{1}+ \left(\frac12 - y_{2}\right) \, \mathbf{a}_{2}- z_{2} \, \mathbf{a}_{3}& = &+ \left(\frac12 + x_{2}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{y}}- z_{2} \, a \, \mathbf{\hat{z}}& \left(12b\right) & \mbox{H} \\ \mathbf{B}_{9} & = &z_{2} \, \mathbf{a}_{1}+ x_{2} \, \mathbf{a}_{2}+ y_{2} \, \mathbf{a}_{3}& = &z_{2} \, a \, \mathbf{\hat{x}}+ x_{2} \, a \, \mathbf{\hat{y}}+ y_{2} \, a \, \mathbf{\hat{z}}& \left(12b\right) & \mbox{H} \\ \mathbf{B}_{10} & = &\left(\frac12 - z_{2}\right) \, \mathbf{a}_{1}- x_{2} \, \mathbf{a}_{2}+ \left(\frac12 + y_{2}\right) \, \mathbf{a}_{3}& = &\left(\frac12 - z_{2}\right) \, a \, \mathbf{\hat{x}}- x_{2} \, a \, \mathbf{\hat{y}}+ \left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{z}}& \left(12b\right) & \mbox{H} \\ \mathbf{B}_{11} & = &- z_{2} \, \mathbf{a}_{1}+ \left(\frac12 + x_{2}\right) \, \mathbf{a}_{2}+ \left(\frac12 - y_{2}\right) \, \mathbf{a}_{3}& = &- z_{2} \, a \, \mathbf{\hat{x}}+ \left(\frac12 + x_{2}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{z}}& \left(12b\right) & \mbox{H} \\ \mathbf{B}_{12} & = &+ \left(\frac12 + z_{2}\right) \, \mathbf{a}_{1}+ \left(\frac12 - x_{2}\right) \, \mathbf{a}_{2}- y_{2} \, \mathbf{a}_{3}& = &+ \left(\frac12 + z_{2}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - x_{2}\right) \, a \, \mathbf{\hat{y}}- y_{2} \, a \, \mathbf{\hat{z}}& \left(12b\right) & \mbox{H} \\ \mathbf{B}_{13} & = &y_{2} \, \mathbf{a}_{1}+ z_{2} \, \mathbf{a}_{2}+ x_{2} \, \mathbf{a}_{3}& = &y_{2} \, a \, \mathbf{\hat{x}}+ z_{2} \, a \, \mathbf{\hat{y}}+ x_{2} \, a \, \mathbf{\hat{z}}& \left(12b\right) & \mbox{H} \\ \mathbf{B}_{14} & = &\left(\frac12 - y_{2}\right) \, \mathbf{a}_{1}- z_{2} \, \mathbf{a}_{2}+ \left(\frac12 + x_{2}\right) \, \mathbf{a}_{3}& = &\left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{x}}- z_{2} \, a \, \mathbf{\hat{y}}+ \left(\frac12 + x_{2}\right) \, a \, \mathbf{\hat{z}}& \left(12b\right) & \mbox{H} \\ \mathbf{B}_{15} & = &- y_{2} \, \mathbf{a}_{1}+ \left(\frac12 + z_{2}\right) \, \mathbf{a}_{2}+ \left(\frac12 - x_{2}\right) \, \mathbf{a}_{3}& = &- y_{2} \, a \, \mathbf{\hat{x}}+ \left(\frac12 + z_{2}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac12 - x_{2}\right) \, a \, \mathbf{\hat{z}}& \left(12b\right) & \mbox{H} \\ \mathbf{B}_{16} & = &+ \left(\frac12 + y_{2}\right) \, \mathbf{a}_{1}+ \left(\frac12 - z_{2}\right) \, \mathbf{a}_{2}- x_{2} \, \mathbf{a}_{3}& = &+ \left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - z_{2}\right) \, a \, \mathbf{\hat{y}}- x_{2} \, a \, \mathbf{\hat{z}}& \left(12b\right) & \mbox{H} \\ \end{array} \]References
- R. Boese, N. Niederprüm, D. Bläser, A. Maulitz, M. Y. Antipin, and P. R. Mallinson, Single–Crystal Structure and Electron Density Distribution of Ammonia at 160 K on the Basis of X–ray Diffraction Data, J. Phys. Chem. B 101, 5794–5799 (1997), doi:10.1021/jp970580v.
- P. P. Ewald and C. Hermann, eds., Strukturbericht 1913-1928, (Akademische Verlagsgesellschaft M. B. H., Leipzig, 1931).
- C. Hermann, O. Lohrmann, and H. Philipp, eds., Strukturbericht Band II 1928-1932 (Akademische Verlagsgesellschaft M. B. H., Leipzig, 1937).