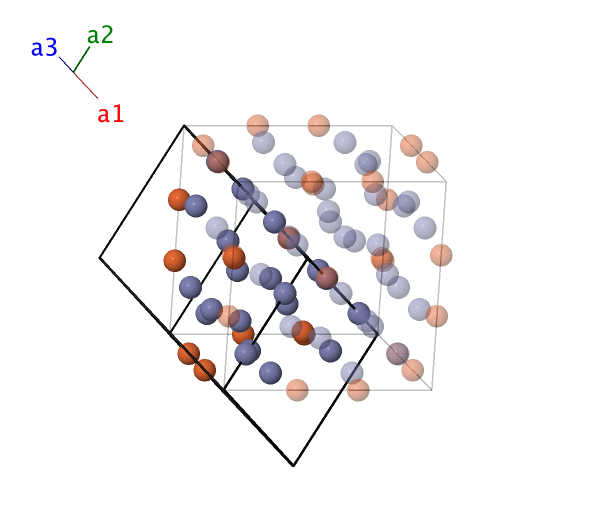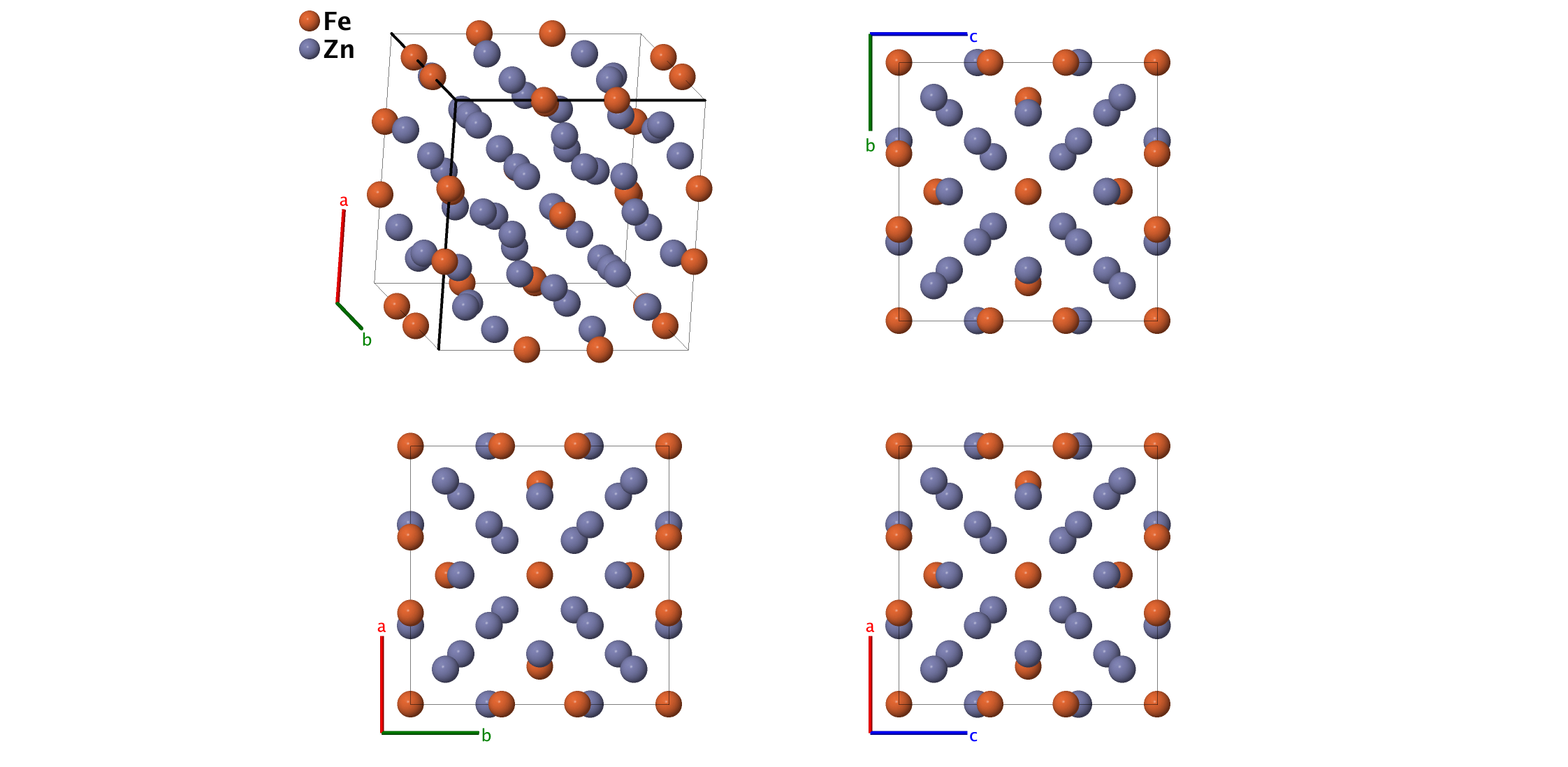
$\gamma$–brass (Fe3Zn10, $D8_{1}$) Structure: A3B10_cI52_229_e_fh
| Prototype | : | Fe3Zn10 |
| AFLOW prototype label | : | A3B10_cI52_229_e_fh |
| Strukturbericht designation | : | $D8_{1}$ |
| Pearson symbol | : | cI52 |
| Space group number | : | 229 |
| Space group symbol | : | $Im\bar{3}m$ |
| AFLOW prototype command | : | aflow --proto=A3B10_cI52_229_e_fh --params=$a,x_{1},x_{2},y_{3}$ |
Other compounds with this structure
- (Pearson, 1958), pp. 252, gives a list of compounds which can take on the D81, D82, or D83 structure, depending on the exact composition.
- Adding another atom at the origin changes this to the $L2_{2}$ structure. This structure is defined in (Pearson, 1958) quoting (Schramm, 1938). More recent investigations such as (Johansson, 1968), (Brandon, 1974) and (Yu, 2005) find that $\gamma$–Fe3Zn10 forms in the $D8_{2}$ structure, with Fe atoms on one (8c) site, Zn atoms on the other (8e) site and the (24g) sites, and a 50-50 alloy of Fe and Zn on the other (8e) site. We use Brandon's data, mapping (12g) $\rightarrow$ (12e), (24g) $\rightarrow$ (24h), and averaging the two (8e) sites to produce the (12e) coordinate here.
Body-centered Cubic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & - \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, a \, \mathbf{\hat{y}} + \frac12 \, a \, \mathbf{\hat{z}} \\
\mathbf{a}_2 & = & ~ \frac12 \, a \, \mathbf{\hat{x}} - \frac12 \, a \, \mathbf{\hat{y}} + \frac12 \, a \, \mathbf{\hat{z}} \\
\mathbf{a}_3 & = & ~ \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, a \, \mathbf{\hat{y}} - \frac12 \, a \, \mathbf{\hat{z}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = & x_{1} \, \mathbf{a}_{2} + x_{1} \, \mathbf{a}_{3} & = & x_{1}a \, \mathbf{\hat{x}} & \left(12e\right) & \mbox{Fe} \\ \mathbf{B}_{2} & = & -x_{1} \, \mathbf{a}_{2}-x_{1} \, \mathbf{a}_{3} & = & -x_{1}a \, \mathbf{\hat{x}} & \left(12e\right) & \mbox{Fe} \\ \mathbf{B}_{3} & = & x_{1} \, \mathbf{a}_{1} + x_{1} \, \mathbf{a}_{3} & = & x_{1}a \, \mathbf{\hat{y}} & \left(12e\right) & \mbox{Fe} \\ \mathbf{B}_{4} & = & -x_{1} \, \mathbf{a}_{1}-x_{1} \, \mathbf{a}_{3} & = & -x_{1}a \, \mathbf{\hat{y}} & \left(12e\right) & \mbox{Fe} \\ \mathbf{B}_{5} & = & x_{1} \, \mathbf{a}_{1} + x_{1} \, \mathbf{a}_{2} & = & x_{1}a \, \mathbf{\hat{z}} & \left(12e\right) & \mbox{Fe} \\ \mathbf{B}_{6} & = & -x_{1} \, \mathbf{a}_{1}-x_{1} \, \mathbf{a}_{2} & = & -x_{1}a \, \mathbf{\hat{z}} & \left(12e\right) & \mbox{Fe} \\ \mathbf{B}_{7} & = & 2x_{2} \, \mathbf{a}_{1} + 2x_{2} \, \mathbf{a}_{2} + 2x_{2} \, \mathbf{a}_{3} & = & x_{2}a \, \mathbf{\hat{x}} + x_{2}a \, \mathbf{\hat{y}} + x_{2}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Zn I} \\ \mathbf{B}_{8} & = & -2x_{2} \, \mathbf{a}_{3} & = & -x_{2}a \, \mathbf{\hat{x}}-x_{2}a \, \mathbf{\hat{y}} + x_{2}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Zn I} \\ \mathbf{B}_{9} & = & -2x_{2} \, \mathbf{a}_{2} & = & -x_{2}a \, \mathbf{\hat{x}} + x_{2}a \, \mathbf{\hat{y}}-x_{2}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Zn I} \\ \mathbf{B}_{10} & = & -2x_{2} \, \mathbf{a}_{1} & = & x_{2}a \, \mathbf{\hat{x}}-x_{2}a \, \mathbf{\hat{y}}-x_{2}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Zn I} \\ \mathbf{B}_{11} & = & 2x_{2} \, \mathbf{a}_{3} & = & x_{2}a \, \mathbf{\hat{x}} + x_{2}a \, \mathbf{\hat{y}}-x_{2}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Zn I} \\ \mathbf{B}_{12} & = & -2x_{2} \, \mathbf{a}_{1}-2x_{2} \, \mathbf{a}_{2}-2x_{2} \, \mathbf{a}_{3} & = & -x_{2}a \, \mathbf{\hat{x}}-x_{2}a \, \mathbf{\hat{y}}-x_{2}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Zn I} \\ \mathbf{B}_{13} & = & 2x_{2} \, \mathbf{a}_{2} & = & x_{2}a \, \mathbf{\hat{x}}-x_{2}a \, \mathbf{\hat{y}} + x_{2}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Zn I} \\ \mathbf{B}_{14} & = & 2x_{2} \, \mathbf{a}_{1} & = & -x_{2}a \, \mathbf{\hat{x}} + x_{2}a \, \mathbf{\hat{y}} + x_{2}a \, \mathbf{\hat{z}} & \left(16f\right) & \mbox{Zn I} \\ \mathbf{B}_{15} & = & 2y_{3} \, \mathbf{a}_{1} + y_{3} \, \mathbf{a}_{2} + y_{3} \, \mathbf{a}_{3} & = & y_{3}a \, \mathbf{\hat{y}} + y_{3}a \, \mathbf{\hat{z}} & \left(24h\right) & \mbox{Zn II} \\ \mathbf{B}_{16} & = & y_{3} \, \mathbf{a}_{2}-y_{3} \, \mathbf{a}_{3} & = & -y_{3}a \, \mathbf{\hat{y}} + y_{3}a \, \mathbf{\hat{z}} & \left(24h\right) & \mbox{Zn II} \\ \mathbf{B}_{17} & = & -y_{3} \, \mathbf{a}_{2} + y_{3} \, \mathbf{a}_{3} & = & y_{3}a \, \mathbf{\hat{y}}-y_{3}a \, \mathbf{\hat{z}} & \left(24h\right) & \mbox{Zn II} \\ \mathbf{B}_{18} & = & -2y_{3} \, \mathbf{a}_{1}-y_{3} \, \mathbf{a}_{2}-y_{3} \, \mathbf{a}_{3} & = & -y_{3}a \, \mathbf{\hat{y}}-y_{3}a \, \mathbf{\hat{z}} & \left(24h\right) & \mbox{Zn II} \\ \mathbf{B}_{19} & = & y_{3} \, \mathbf{a}_{1} + 2y_{3} \, \mathbf{a}_{2} + y_{3} \, \mathbf{a}_{3} & = & y_{3}a \, \mathbf{\hat{x}} + y_{3}a \, \mathbf{\hat{z}} & \left(24h\right) & \mbox{Zn II} \\ \mathbf{B}_{20} & = & -y_{3} \, \mathbf{a}_{1} + y_{3} \, \mathbf{a}_{3} & = & y_{3}a \, \mathbf{\hat{x}}-y_{3}a \, \mathbf{\hat{z}} & \left(24h\right) & \mbox{Zn II} \\ \mathbf{B}_{21} & = & y_{3} \, \mathbf{a}_{1}-y_{3} \, \mathbf{a}_{3} & = & -y_{3}a \, \mathbf{\hat{x}} + y_{3}a \, \mathbf{\hat{z}} & \left(24h\right) & \mbox{Zn II} \\ \mathbf{B}_{22} & = & -y_{3} \, \mathbf{a}_{1}-2y_{3} \, \mathbf{a}_{2}-y_{3} \, \mathbf{a}_{3} & = & -y_{3}a \, \mathbf{\hat{x}}-y_{3}a \, \mathbf{\hat{z}} & \left(24h\right) & \mbox{Zn II} \\ \mathbf{B}_{23} & = & y_{3} \, \mathbf{a}_{1} + y_{3} \, \mathbf{a}_{2} + 2y_{3} \, \mathbf{a}_{3} & = & y_{3}a \, \mathbf{\hat{x}} + y_{3}a \, \mathbf{\hat{y}} & \left(24h\right) & \mbox{Zn II} \\ \mathbf{B}_{24} & = & y_{3} \, \mathbf{a}_{1}-y_{3} \, \mathbf{a}_{2} & = & -y_{3}a \, \mathbf{\hat{x}} + y_{3}a \, \mathbf{\hat{y}} & \left(24h\right) & \mbox{Zn II} \\ \mathbf{B}_{25} & = & -y_{3} \, \mathbf{a}_{1} + y_{3} \, \mathbf{a}_{2} & = & y_{3}a \, \mathbf{\hat{x}}-y_{3}a \, \mathbf{\hat{y}} & \left(24h\right) & \mbox{Zn II} \\ \mathbf{B}_{26} & = & -y_{3} \, \mathbf{a}_{1}-y_{3} \, \mathbf{a}_{2}-2y_{3} \, \mathbf{a}_{3} & = & -y_{3}a \, \mathbf{\hat{x}}-y_{3}a \, \mathbf{\hat{y}} & \left(24h\right) & \mbox{Zn II} \\ \end{array} \]References
- J. Schramm, X–Ray Investigation of Phases and Phase Limits of the Zn Alloy Systems with Fe, Co and Ni, Z. Metallkd. 30, 122–130 (1938).
- A. Johansson, H. Ljung, and S. Westman, X–Ray and Neutron Diffraction Studies on Gamma–Ni,Zn and Gamma–Fe,Zn, Acta Chem. Scand. 22, 2743–2753 (1968), doi:10.3891/acta.chem.scand.22-2743.
- J. K. Brandon, R. Y. Brizard, P. C. Chieh, R. K. McMillan, and W. B. Pearson, New refinements of the γ–brass type structures Cu5Zn8, Cu5Cd8 and Fe3Zn10, Acta Crystallogr. Sect. B Struct. Sci. 30, 1412–1417 (1974), doi:10.1107/S0567740874004997.
- J. Yu, J. Liu, J. Zhang, and J. Wu, Electron Diffraction Study on Fe–Zn Gamma intermetallic Phase of a Galvannealed IF Steel Sheet, Mater. Trans. 46, 1079–1082 (2005), doi:10.2320/matertrans.46.1079.
Found in
- W. B. Pearson, A Handbook of Lattice Spacings and Structures of Metals and Alloys, no. N.R.C. No. 4303 in International Series of Monographs on Metal Physics and Physical Metallurgy (Pergamon Press, Oxford, London, Edinburgh, New York, Paris, Frankfort, 1958), 1964 reprint with corrections edn.