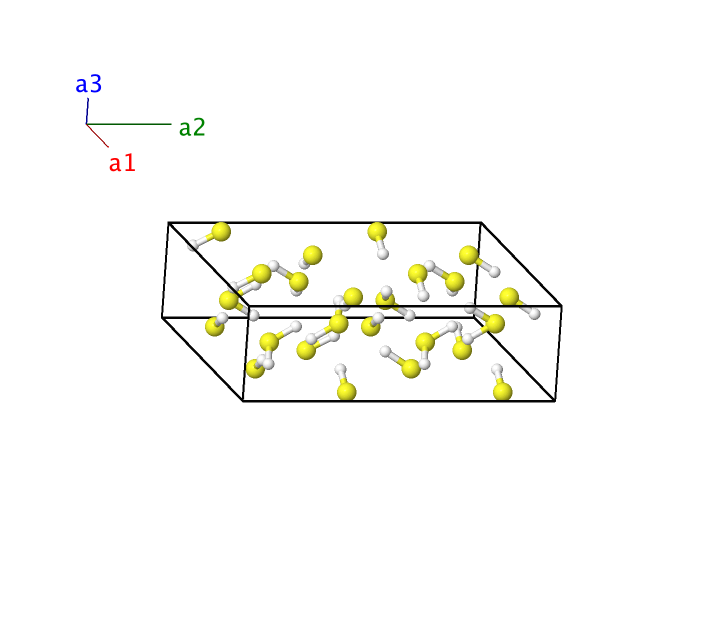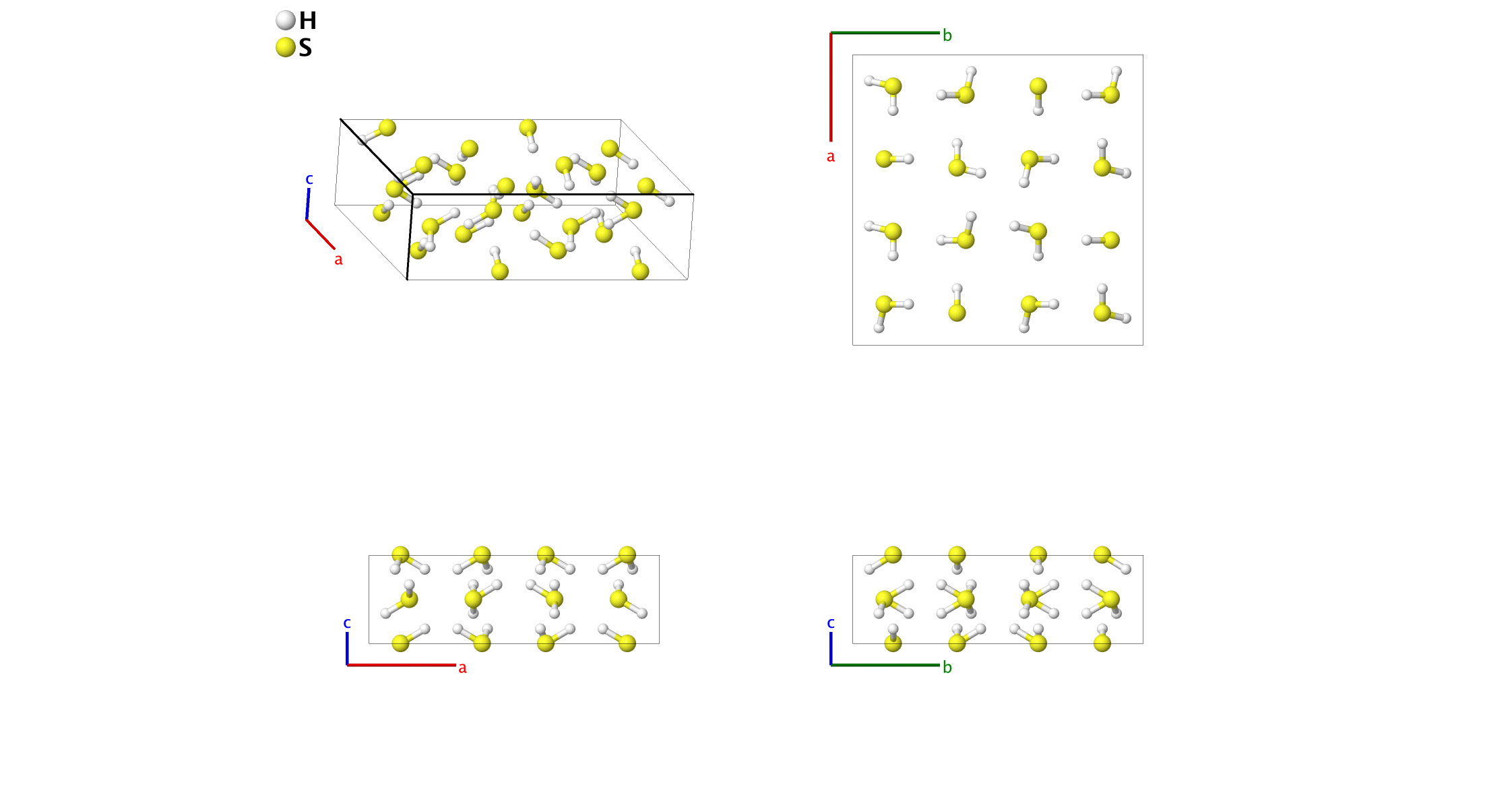
H2S III Structure: A2B_tP48_77_8d_4d
| Prototype | : | H2S |
| AFLOW prototype label | : | A2B_tP48_77_8d_4d |
| Strukturbericht designation | : | None |
| Pearson symbol | : | tP48 |
| Space group number | : | 77 |
| Space group symbol | : | $P4_{2}$ |
| AFLOW prototype command | : | aflow --proto=A2B_tP48_77_8d_4d --params=$a,c/a,x_{1},y_{1},z_{1},x_{2},y_{2},z_{2},x_{3},y_{3},z_{3},x_{4},y_{4},z_{4},x_{5},y_{5},z_{5},x_{6},y_{6},z_{6},x_{7}, \\y_{7},z_{7},x_{8},y_{8},z_{8},x_{9},y_{9},z_{9},x_{10},y_{10},z_{10},x_{11},y_{11},z_{11},x_{12},y_{12},z_{12}$ |
- This is one candidate structure for the H2S III structure, which is stable at pressures under 4 GPa and temperatures less than $\approx 100 K (Shimizu, 1995). The data presented here was for D2S at 102 K and ambient pressure.
Simple Tetragonal primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \\
\mathbf{a}_2 & = & a \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \, \mathbf{\hat{z}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = & x_{1} \, \mathbf{a}_{1} + y_{1} \, \mathbf{a}_{2} + z_{1} \, \mathbf{a}_{3} & = & x_{1}a \, \mathbf{\hat{x}} + y_{1}a \, \mathbf{\hat{y}} + z_{1}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H I} \\ \mathbf{B}_{2} & = & -x_{1} \, \mathbf{a}_{1}-y_{1} \, \mathbf{a}_{2} + z_{1} \, \mathbf{a}_{3} & = & -x_{1}a \, \mathbf{\hat{x}}-y_{1}a \, \mathbf{\hat{y}} + z_{1}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H I} \\ \mathbf{B}_{3} & = & -y_{1} \, \mathbf{a}_{1} + x_{1} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{1}\right) \, \mathbf{a}_{3} & = & -y_{1}a \, \mathbf{\hat{x}} + x_{1}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{1}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H I} \\ \mathbf{B}_{4} & = & y_{1} \, \mathbf{a}_{1}-x_{1} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{1}\right) \, \mathbf{a}_{3} & = & y_{1}a \, \mathbf{\hat{x}}-x_{1}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{1}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H I} \\ \mathbf{B}_{5} & = & x_{2} \, \mathbf{a}_{1} + y_{2} \, \mathbf{a}_{2} + z_{2} \, \mathbf{a}_{3} & = & x_{2}a \, \mathbf{\hat{x}} + y_{2}a \, \mathbf{\hat{y}} + z_{2}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H II} \\ \mathbf{B}_{6} & = & -x_{2} \, \mathbf{a}_{1}-y_{2} \, \mathbf{a}_{2} + z_{2} \, \mathbf{a}_{3} & = & -x_{2}a \, \mathbf{\hat{x}}-y_{2}a \, \mathbf{\hat{y}} + z_{2}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H II} \\ \mathbf{B}_{7} & = & -y_{2} \, \mathbf{a}_{1} + x_{2} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{2}\right) \, \mathbf{a}_{3} & = & -y_{2}a \, \mathbf{\hat{x}} + x_{2}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{2}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H II} \\ \mathbf{B}_{8} & = & y_{2} \, \mathbf{a}_{1}-x_{2} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{2}\right) \, \mathbf{a}_{3} & = & y_{2}a \, \mathbf{\hat{x}}-x_{2}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{2}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H II} \\ \mathbf{B}_{9} & = & x_{3} \, \mathbf{a}_{1} + y_{3} \, \mathbf{a}_{2} + z_{3} \, \mathbf{a}_{3} & = & x_{3}a \, \mathbf{\hat{x}} + y_{3}a \, \mathbf{\hat{y}} + z_{3}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H III} \\ \mathbf{B}_{10} & = & -x_{3} \, \mathbf{a}_{1}-y_{3} \, \mathbf{a}_{2} + z_{3} \, \mathbf{a}_{3} & = & -x_{3}a \, \mathbf{\hat{x}}-y_{3}a \, \mathbf{\hat{y}} + z_{3}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H III} \\ \mathbf{B}_{11} & = & -y_{3} \, \mathbf{a}_{1} + x_{3} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{3}\right) \, \mathbf{a}_{3} & = & -y_{3}a \, \mathbf{\hat{x}} + x_{3}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{3}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H III} \\ \mathbf{B}_{12} & = & y_{3} \, \mathbf{a}_{1}-x_{3} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{3}\right) \, \mathbf{a}_{3} & = & y_{3}a \, \mathbf{\hat{x}}-x_{3}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{3}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H III} \\ \mathbf{B}_{13} & = & x_{4} \, \mathbf{a}_{1} + y_{4} \, \mathbf{a}_{2} + z_{4} \, \mathbf{a}_{3} & = & x_{4}a \, \mathbf{\hat{x}} + y_{4}a \, \mathbf{\hat{y}} + z_{4}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H IV} \\ \mathbf{B}_{14} & = & -x_{4} \, \mathbf{a}_{1}-y_{4} \, \mathbf{a}_{2} + z_{4} \, \mathbf{a}_{3} & = & -x_{4}a \, \mathbf{\hat{x}}-y_{4}a \, \mathbf{\hat{y}} + z_{4}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H IV} \\ \mathbf{B}_{15} & = & -y_{4} \, \mathbf{a}_{1} + x_{4} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{4}\right) \, \mathbf{a}_{3} & = & -y_{4}a \, \mathbf{\hat{x}} + x_{4}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{4}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H IV} \\ \mathbf{B}_{16} & = & y_{4} \, \mathbf{a}_{1}-x_{4} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{4}\right) \, \mathbf{a}_{3} & = & y_{4}a \, \mathbf{\hat{x}}-x_{4}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{4}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H IV} \\ \mathbf{B}_{17} & = & x_{5} \, \mathbf{a}_{1} + y_{5} \, \mathbf{a}_{2} + z_{5} \, \mathbf{a}_{3} & = & x_{5}a \, \mathbf{\hat{x}} + y_{5}a \, \mathbf{\hat{y}} + z_{5}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H V} \\ \mathbf{B}_{18} & = & -x_{5} \, \mathbf{a}_{1}-y_{5} \, \mathbf{a}_{2} + z_{5} \, \mathbf{a}_{3} & = & -x_{5}a \, \mathbf{\hat{x}}-y_{5}a \, \mathbf{\hat{y}} + z_{5}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H V} \\ \mathbf{B}_{19} & = & -y_{5} \, \mathbf{a}_{1} + x_{5} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{5}\right) \, \mathbf{a}_{3} & = & -y_{5}a \, \mathbf{\hat{x}} + x_{5}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{5}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H V} \\ \mathbf{B}_{20} & = & y_{5} \, \mathbf{a}_{1}-x_{5} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{5}\right) \, \mathbf{a}_{3} & = & y_{5}a \, \mathbf{\hat{x}}-x_{5}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{5}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H V} \\ \mathbf{B}_{21} & = & x_{6} \, \mathbf{a}_{1} + y_{6} \, \mathbf{a}_{2} + z_{6} \, \mathbf{a}_{3} & = & x_{6}a \, \mathbf{\hat{x}} + y_{6}a \, \mathbf{\hat{y}} + z_{6}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H VI} \\ \mathbf{B}_{22} & = & -x_{6} \, \mathbf{a}_{1}-y_{6} \, \mathbf{a}_{2} + z_{6} \, \mathbf{a}_{3} & = & -x_{6}a \, \mathbf{\hat{x}}-y_{6}a \, \mathbf{\hat{y}} + z_{6}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H VI} \\ \mathbf{B}_{23} & = & -y_{6} \, \mathbf{a}_{1} + x_{6} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{6}\right) \, \mathbf{a}_{3} & = & -y_{6}a \, \mathbf{\hat{x}} + x_{6}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{6}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H VI} \\ \mathbf{B}_{24} & = & y_{6} \, \mathbf{a}_{1}-x_{6} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{6}\right) \, \mathbf{a}_{3} & = & y_{6}a \, \mathbf{\hat{x}}-x_{6}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{6}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H VI} \\ \mathbf{B}_{25} & = & x_{7} \, \mathbf{a}_{1} + y_{7} \, \mathbf{a}_{2} + z_{7} \, \mathbf{a}_{3} & = & x_{7}a \, \mathbf{\hat{x}} + y_{7}a \, \mathbf{\hat{y}} + z_{7}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H VII} \\ \mathbf{B}_{26} & = & -x_{7} \, \mathbf{a}_{1}-y_{7} \, \mathbf{a}_{2} + z_{7} \, \mathbf{a}_{3} & = & -x_{7}a \, \mathbf{\hat{x}}-y_{7}a \, \mathbf{\hat{y}} + z_{7}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H VII} \\ \mathbf{B}_{27} & = & -y_{7} \, \mathbf{a}_{1} + x_{7} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{7}\right) \, \mathbf{a}_{3} & = & -y_{7}a \, \mathbf{\hat{x}} + x_{7}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{7}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H VII} \\ \mathbf{B}_{28} & = & y_{7} \, \mathbf{a}_{1}-x_{7} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{7}\right) \, \mathbf{a}_{3} & = & y_{7}a \, \mathbf{\hat{x}}-x_{7}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{7}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H VII} \\ \mathbf{B}_{29} & = & x_{8} \, \mathbf{a}_{1} + y_{8} \, \mathbf{a}_{2} + z_{8} \, \mathbf{a}_{3} & = & x_{8}a \, \mathbf{\hat{x}} + y_{8}a \, \mathbf{\hat{y}} + z_{8}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H VIII} \\ \mathbf{B}_{30} & = & -x_{8} \, \mathbf{a}_{1}-y_{8} \, \mathbf{a}_{2} + z_{8} \, \mathbf{a}_{3} & = & -x_{8}a \, \mathbf{\hat{x}}-y_{8}a \, \mathbf{\hat{y}} + z_{8}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H VIII} \\ \mathbf{B}_{31} & = & -y_{8} \, \mathbf{a}_{1} + x_{8} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{8}\right) \, \mathbf{a}_{3} & = & -y_{8}a \, \mathbf{\hat{x}} + x_{8}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{8}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H VIII} \\ \mathbf{B}_{32} & = & y_{8} \, \mathbf{a}_{1}-x_{8} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{8}\right) \, \mathbf{a}_{3} & = & y_{8}a \, \mathbf{\hat{x}}-x_{8}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{8}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{H VIII} \\ \mathbf{B}_{33} & = & x_{9} \, \mathbf{a}_{1} + y_{9} \, \mathbf{a}_{2} + z_{9} \, \mathbf{a}_{3} & = & x_{9}a \, \mathbf{\hat{x}} + y_{9}a \, \mathbf{\hat{y}} + z_{9}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S I} \\ \mathbf{B}_{34} & = & -x_{9} \, \mathbf{a}_{1}-y_{9} \, \mathbf{a}_{2} + z_{9} \, \mathbf{a}_{3} & = & -x_{9}a \, \mathbf{\hat{x}}-y_{9}a \, \mathbf{\hat{y}} + z_{9}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S I} \\ \mathbf{B}_{35} & = & -y_{9} \, \mathbf{a}_{1} + x_{9} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{9}\right) \, \mathbf{a}_{3} & = & -y_{9}a \, \mathbf{\hat{x}} + x_{9}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{9}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S I} \\ \mathbf{B}_{36} & = & y_{9} \, \mathbf{a}_{1}-x_{9} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{9}\right) \, \mathbf{a}_{3} & = & y_{9}a \, \mathbf{\hat{x}}-x_{9}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{9}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S I} \\ \mathbf{B}_{37} & = & x_{10} \, \mathbf{a}_{1} + y_{10} \, \mathbf{a}_{2} + z_{10} \, \mathbf{a}_{3} & = & x_{10}a \, \mathbf{\hat{x}} + y_{10}a \, \mathbf{\hat{y}} + z_{10}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S II} \\ \mathbf{B}_{38} & = & -x_{10} \, \mathbf{a}_{1}-y_{10} \, \mathbf{a}_{2} + z_{10} \, \mathbf{a}_{3} & = & -x_{10}a \, \mathbf{\hat{x}}-y_{10}a \, \mathbf{\hat{y}} + z_{10}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S II} \\ \mathbf{B}_{39} & = & -y_{10} \, \mathbf{a}_{1} + x_{10} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{10}\right) \, \mathbf{a}_{3} & = & -y_{10}a \, \mathbf{\hat{x}} + x_{10}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{10}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S II} \\ \mathbf{B}_{40} & = & y_{10} \, \mathbf{a}_{1}-x_{10} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{10}\right) \, \mathbf{a}_{3} & = & y_{10}a \, \mathbf{\hat{x}}-x_{10}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{10}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S II} \\ \mathbf{B}_{41} & = & x_{11} \, \mathbf{a}_{1} + y_{11} \, \mathbf{a}_{2} + z_{11} \, \mathbf{a}_{3} & = & x_{11}a \, \mathbf{\hat{x}} + y_{11}a \, \mathbf{\hat{y}} + z_{11}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S III} \\ \mathbf{B}_{42} & = & -x_{11} \, \mathbf{a}_{1}-y_{11} \, \mathbf{a}_{2} + z_{11} \, \mathbf{a}_{3} & = & -x_{11}a \, \mathbf{\hat{x}}-y_{11}a \, \mathbf{\hat{y}} + z_{11}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S III} \\ \mathbf{B}_{43} & = & -y_{11} \, \mathbf{a}_{1} + x_{11} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{11}\right) \, \mathbf{a}_{3} & = & -y_{11}a \, \mathbf{\hat{x}} + x_{11}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{11}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S III} \\ \mathbf{B}_{44} & = & y_{11} \, \mathbf{a}_{1}-x_{11} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{11}\right) \, \mathbf{a}_{3} & = & y_{11}a \, \mathbf{\hat{x}}-x_{11}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{11}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S III} \\ \mathbf{B}_{45} & = & x_{12} \, \mathbf{a}_{1} + y_{12} \, \mathbf{a}_{2} + z_{12} \, \mathbf{a}_{3} & = & x_{12}a \, \mathbf{\hat{x}} + y_{12}a \, \mathbf{\hat{y}} + z_{12}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S IV} \\ \mathbf{B}_{46} & = & -x_{12} \, \mathbf{a}_{1}-y_{12} \, \mathbf{a}_{2} + z_{12} \, \mathbf{a}_{3} & = & -x_{12}a \, \mathbf{\hat{x}}-y_{12}a \, \mathbf{\hat{y}} + z_{12}c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S IV} \\ \mathbf{B}_{47} & = & -y_{12} \, \mathbf{a}_{1} + x_{12} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{12}\right) \, \mathbf{a}_{3} & = & -y_{12}a \, \mathbf{\hat{x}} + x_{12}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{12}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S IV} \\ \mathbf{B}_{48} & = & y_{12} \, \mathbf{a}_{1}-x_{12} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{12}\right) \, \mathbf{a}_{3} & = & y_{12}a \, \mathbf{\hat{x}}-x_{12}a \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{12}\right)c \, \mathbf{\hat{z}} & \left(4d\right) & \mbox{S IV} \\ \end{array} \]References
- E. Sándor and S. O. Ogunade, Structure and Phase Transition in Solid Hydrogen and Deuterium Sulphides, Nature 224, 905–907 (1969), doi:10.1038/224905b0.
Found in
- H. Shimizu, H. Yamaguchi, S. Sasaki, A. Honda, S. Endo, and M. Kobayashi, Pressure–temperature phase diagram of solid hydrogen sulfide determined by Raman spectroscopy, Phys. Rev. B 51, 9391–9394 (1995), doi:10.1103/PhysRevB.51.9391.