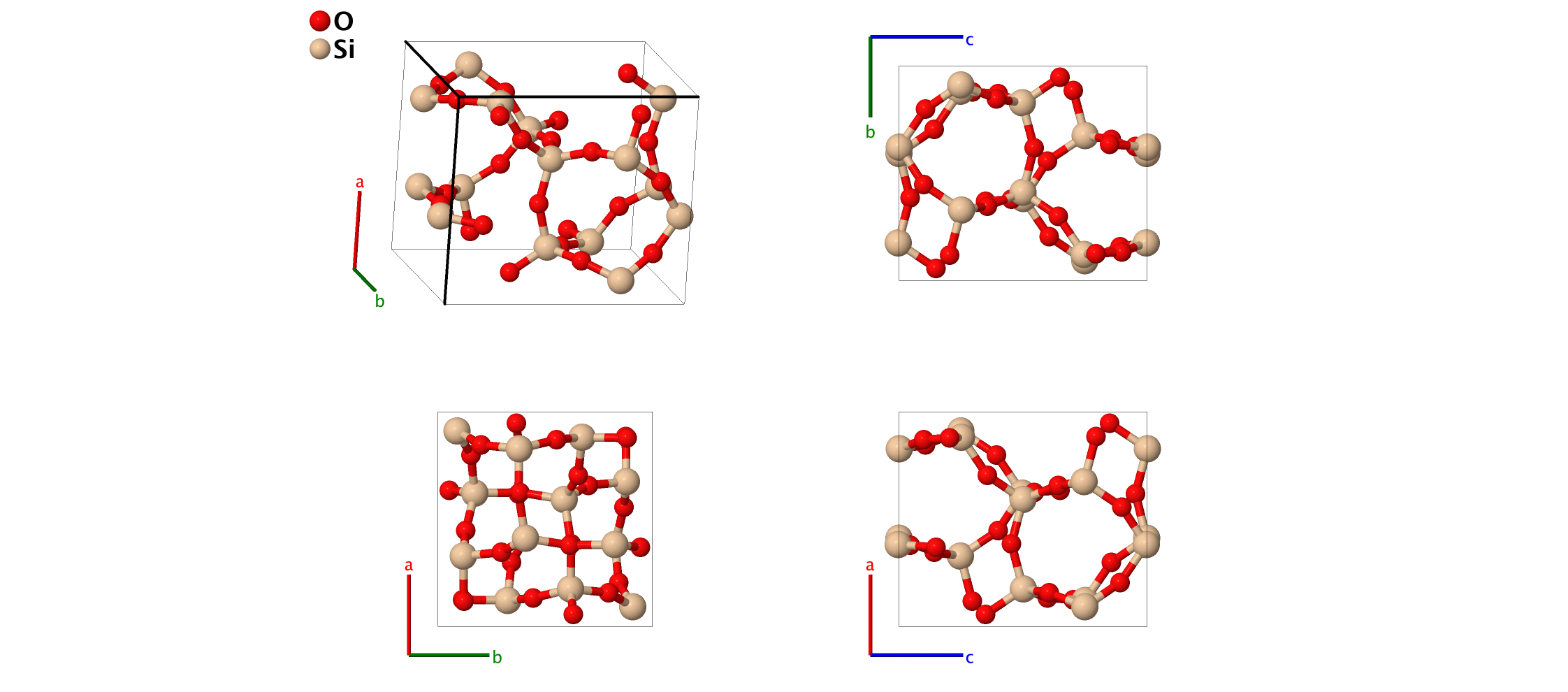
Keatite (SiO2) Structure: A2B_tP36_96_3b_ab
| Prototype | : | SiO2 |
| AFLOW prototype label | : | A2B_tP36_96_3b_ab |
| Strukturbericht designation | : | None |
| Pearson symbol | : | tP36 |
| Space group number | : | 96 |
| Space group symbol | : | $\mbox{P4}_{3}\mbox{2}_{1}\mbox{2}$ |
| AFLOW prototype command | : | aflow --proto=A2B_tP36_96_3b_ab --params=$a,c/a,x_{1},x_{2},y_{2},z_{2},x_{3},y_{3},z_{3},x_{4},y_{4},z_{4},x_{5},y_{5},z_{5}$ |
- All references, including (Wyckoff, 1963), (Shropshire, 1959) and (Demuth, 1999) note that keatite can exist in both space group P41212–D44 (#92) and its enantiomorph P43212–D48 (#96). Wyckoff uses the coordinates proposed by Shropshire and assumes the space group is P41212. He then notes that one of the Si–O bonds in this structure is very long (3.69 Å), and is
so improbable that there is something wrong either with the parameters as stated or the structure itself
. If we use space group P43212 while retaining Shropshire's coordinates we obtain a much more convincing structure, one that looks much like the structure in Shropshire's Fig. 3. For this reason we place this structure in P43212.
Simple Tetragonal primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \\
\mathbf{a}_2 & = & a \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \, \mathbf{\hat{z}}\\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & =&x_{1} \, \mathbf{a}_{1}+ x_{1} \, \mathbf{a}_{2}& =&x_{1} \, a \, \mathbf{\hat{x}}+ x_{1} \, a \, \mathbf{\hat{y}}& \left(4a\right) & \mbox{Si I} \\ \mathbf{B}_{2} & =&- x_{1} \, \mathbf{a}_{1}- x_{1} \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& =&- x_{1} \, a \, \mathbf{\hat{x}}- x_{1} \, a \, \mathbf{\hat{y}}+ \frac12 \, c \, \mathbf{\hat{z}}& \left(4a\right) & \mbox{Si I} \\ \mathbf{B}_{3} & =&\left(\frac12 - x_{1}\right) \, \mathbf{a}_{1}+ \left(\frac12 + x_{1}\right) \, \mathbf{a}_{2}+ \frac34 \, \mathbf{a}_{3}& =&\left(\frac12 - x_{1}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 + x_{1}\right) \, a \, \mathbf{\hat{y}}+ \frac34 \, c \, \mathbf{\hat{z}}& \left(4a\right) & \mbox{Si I} \\ \mathbf{B}_{4} & =&\left(\frac12 + x_{1}\right) \, \mathbf{a}_{1}+ \left(\frac12 - x_{1}\right) \, \mathbf{a}_{2}+ \frac14 \, \mathbf{a}_{3}& =&\left(\frac12 + x_{1}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - x_{1}\right) \, a \, \mathbf{\hat{y}}+ \frac14 \, c \, \mathbf{\hat{z}}& \left(4a\right) & \mbox{Si I} \\ \mathbf{B}_{5} & =&x_{2} \, \mathbf{a}_{1}+ y_{2} \, \mathbf{a}_{2}+ z_{2} \, \mathbf{a}_{3}& =&x_{2} \, a \, \mathbf{\hat{x}}+ y_{2} \, a \, \mathbf{\hat{y}}+ z_{2} \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O I} \\ \mathbf{B}_{6} & =&- x_{2} \, \mathbf{a}_{1}- y_{2} \, \mathbf{a}_{2}+ \left(\frac12 + z_{2}\right) \, \mathbf{a}_{3}& =&- x_{2} \, a \, \mathbf{\hat{x}}- y_{2} \, a \, \mathbf{\hat{y}}+ \left(\frac12 + z_{2}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O I} \\ \mathbf{B}_{7} & =&\left(\frac12 - y_{2}\right) \, \mathbf{a}_{1}+ \left(\frac12 + x_{2}\right) \, \mathbf{a}_{2}+ \left(\frac34 + z_{2}\right) \, \mathbf{a}_{3}& =&\left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 + x_{2}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac34 + z_{2}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O I} \\ \mathbf{B}_{8} & =&\left(\frac12 + y_{2}\right) \, \mathbf{a}_{1}+ \left(\frac12 - x_{2}\right) \, \mathbf{a}_{2}+ \left(\frac14 + z_{2}\right) \, \mathbf{a}_{3}& =&\left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - x_{2}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 + z_{2}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O I} \\ \mathbf{B}_{9} & =&\left(\frac12 - x_{2}\right) \, \mathbf{a}_{1}+ \left(\frac12 + y_{2}\right) \, \mathbf{a}_{2}+ \left(\frac34 - z_{2}\right) \, \mathbf{a}_{3}& =&\left(\frac12 - x_{2}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac34 - z_{2}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O I} \\ \mathbf{B}_{10} & =&\left(\frac12 + x_{2}\right) \, \mathbf{a}_{1}+ \left(\frac12 - y_{2}\right) \, \mathbf{a}_{2}+ \left(\frac14 - z_{2}\right) \, \mathbf{a}_{3}& =&\left(\frac12 + x_{2}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 - z_{2}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O I} \\ \mathbf{B}_{11} & =&y_{2} \, \mathbf{a}_{1}+ x_{2} \, \mathbf{a}_{2}- z_{2} \, \mathbf{a}_{3}& =&y_{2} \, a \, \mathbf{\hat{x}}+ x_{2} \, a \, \mathbf{\hat{y}}- z_{2} \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O I} \\ \mathbf{B}_{12} & =&- y_{2} \, \mathbf{a}_{1}- x_{2} \, \mathbf{a}_{2}+ \left(\frac12 - z_{2}\right) \, \mathbf{a}_{3}& =&- y_{2} \, a \, \mathbf{\hat{x}}- x_{2} \, a \, \mathbf{\hat{y}}+ \left(\frac12 - z_{2}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O I} \\ \mathbf{B}_{13} & =&x_{3} \, \mathbf{a}_{1}+ y_{3} \, \mathbf{a}_{2}+ z_{3} \, \mathbf{a}_{3}& =&x_{3} \, a \, \mathbf{\hat{x}}+ y_{3} \, a \, \mathbf{\hat{y}}+ z_{3} \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O II} \\ \mathbf{B}_{14} & =&- x_{3} \, \mathbf{a}_{1}- y_{3} \, \mathbf{a}_{2}+ \left(\frac12 + z_{3}\right) \, \mathbf{a}_{3}& =&- x_{3} \, a \, \mathbf{\hat{x}}- y_{3} \, a \, \mathbf{\hat{y}}+ \left(\frac12 + z_{3}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O II} \\ \mathbf{B}_{15} & =&\left(\frac12 - y_{3}\right) \, \mathbf{a}_{1}+ \left(\frac12 + x_{3}\right) \, \mathbf{a}_{2}+ \left(\frac34 + z_{3}\right) \, \mathbf{a}_{3}& =&\left(\frac12 - y_{3}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 + x_{3}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac34 + z_{3}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O II} \\ \mathbf{B}_{16} & =&\left(\frac12 + y_{3}\right) \, \mathbf{a}_{1}+ \left(\frac12 - x_{3}\right) \, \mathbf{a}_{2}+ \left(\frac14 + z_{3}\right) \, \mathbf{a}_{3}& =&\left(\frac12 + y_{3}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - x_{3}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 + z_{3}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O II} \\ \mathbf{B}_{17} & =&\left(\frac12 - x_{3}\right) \, \mathbf{a}_{1}+ \left(\frac12 + y_{3}\right) \, \mathbf{a}_{2}+ \left(\frac34 - z_{3}\right) \, \mathbf{a}_{3}& =&\left(\frac12 - x_{3}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 + y_{3}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac34 - z_{3}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O II} \\ \mathbf{B}_{18} & =&\left(\frac12 + x_{3}\right) \, \mathbf{a}_{1}+ \left(\frac12 - y_{3}\right) \, \mathbf{a}_{2}+ \left(\frac14 - z_{3}\right) \, \mathbf{a}_{3}& =&\left(\frac12 + x_{3}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - y_{3}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 - z_{3}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O II} \\ \mathbf{B}_{19} & =&y_{3} \, \mathbf{a}_{1}+ x_{3} \, \mathbf{a}_{2}- z_{3} \, \mathbf{a}_{3}& =&y_{3} \, a \, \mathbf{\hat{x}}+ x_{3} \, a \, \mathbf{\hat{y}}- z_{3} \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O II} \\ \mathbf{B}_{20} & =&- y_{3} \, \mathbf{a}_{1}- x_{3} \, \mathbf{a}_{2}+ \left(\frac12 - z_{3}\right) \, \mathbf{a}_{3}& =&- y_{3} \, a \, \mathbf{\hat{x}}- x_{3} \, a \, \mathbf{\hat{y}}+ \left(\frac12 - z_{3}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O II} \\ \mathbf{B}_{21} & =&x_{4} \, \mathbf{a}_{1}+ y_{4} \, \mathbf{a}_{2}+ z_{4} \, \mathbf{a}_{3}& =&x_{4} \, a \, \mathbf{\hat{x}}+ y_{4} \, a \, \mathbf{\hat{y}}+ z_{4} \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O III} \\ \mathbf{B}_{22} & =&- x_{4} \, \mathbf{a}_{1}- y_{4} \, \mathbf{a}_{2}+ \left(\frac12 + z_{4}\right) \, \mathbf{a}_{3}& =&- x_{4} \, a \, \mathbf{\hat{x}}- y_{4} \, a \, \mathbf{\hat{y}}+ \left(\frac12 + z_{4}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O III} \\ \mathbf{B}_{23} & =&\left(\frac12 - y_{4}\right) \, \mathbf{a}_{1}+ \left(\frac12 + x_{4}\right) \, \mathbf{a}_{2}+ \left(\frac34 + z_{4}\right) \, \mathbf{a}_{3}& =&\left(\frac12 - y_{4}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 + x_{4}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac34 + z_{4}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O III} \\ \mathbf{B}_{24} & =&\left(\frac12 + y_{4}\right) \, \mathbf{a}_{1}+ \left(\frac12 - x_{4}\right) \, \mathbf{a}_{2}+ \left(\frac14 + z_{4}\right) \, \mathbf{a}_{3}& =&\left(\frac12 + y_{4}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - x_{4}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 + z_{4}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O III} \\ \mathbf{B}_{25} & =&\left(\frac12 - x_{4}\right) \, \mathbf{a}_{1}+ \left(\frac12 + y_{4}\right) \, \mathbf{a}_{2}+ \left(\frac34 - z_{4}\right) \, \mathbf{a}_{3}& =&\left(\frac12 - x_{4}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 + y_{4}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac34 - z_{4}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O III} \\ \mathbf{B}_{26} & =&\left(\frac12 + x_{4}\right) \, \mathbf{a}_{1}+ \left(\frac12 - y_{4}\right) \, \mathbf{a}_{2}+ \left(\frac14 - z_{4}\right) \, \mathbf{a}_{3}& =&\left(\frac12 + x_{4}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - y_{4}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 - z_{4}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O III} \\ \mathbf{B}_{27} & =&y_{4} \, \mathbf{a}_{1}+ x_{4} \, \mathbf{a}_{2}- z_{4} \, \mathbf{a}_{3}& =&y_{4} \, a \, \mathbf{\hat{x}}+ x_{4} \, a \, \mathbf{\hat{y}}- z_{4} \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O III} \\ \mathbf{B}_{28} & =&- y_{4} \, \mathbf{a}_{1}- x_{4} \, \mathbf{a}_{2}+ \left(\frac12 - z_{4}\right) \, \mathbf{a}_{3}& =&- y_{4} \, a \, \mathbf{\hat{x}}- x_{4} \, a \, \mathbf{\hat{y}}+ \left(\frac12 - z_{4}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{O III} \\ \mathbf{B}_{29} & =&x_{5} \, \mathbf{a}_{1}+ y_{5} \, \mathbf{a}_{2}+ z_{5} \, \mathbf{a}_{3}& =&x_{5} \, a \, \mathbf{\hat{x}}+ y_{5} \, a \, \mathbf{\hat{y}}+ z_{5} \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{Si II} \\ \mathbf{B}_{30} & =&- x_{5} \, \mathbf{a}_{1}- y_{5} \, \mathbf{a}_{2}+ \left(\frac12 + z_{5}\right) \, \mathbf{a}_{3}& =&- x_{5} \, a \, \mathbf{\hat{x}}- y_{5} \, a \, \mathbf{\hat{y}}+ \left(\frac12 + z_{5}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{Si II} \\ \mathbf{B}_{31} & =&\left(\frac12 - y_{5}\right) \, \mathbf{a}_{1}+ \left(\frac12 + x_{5}\right) \, \mathbf{a}_{2}+ \left(\frac34 + z_{5}\right) \, \mathbf{a}_{3}& =&\left(\frac12 - y_{5}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 + x_{5}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac34 + z_{5}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{Si II} \\ \mathbf{B}_{32} & =&\left(\frac12 + y_{5}\right) \, \mathbf{a}_{1}+ \left(\frac12 - x_{5}\right) \, \mathbf{a}_{2}+ \left(\frac14 + z_{5}\right) \, \mathbf{a}_{3}& =&\left(\frac12 + y_{5}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - x_{5}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 + z_{5}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{Si II} \\ \mathbf{B}_{33} & =&\left(\frac12 - x_{5}\right) \, \mathbf{a}_{1}+ \left(\frac12 + y_{5}\right) \, \mathbf{a}_{2}+ \left(\frac34 - z_{5}\right) \, \mathbf{a}_{3}& =&\left(\frac12 - x_{5}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 + y_{5}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac34 - z_{5}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{Si II} \\ \mathbf{B}_{34} & =&\left(\frac12 + x_{5}\right) \, \mathbf{a}_{1}+ \left(\frac12 - y_{5}\right) \, \mathbf{a}_{2}+ \left(\frac14 - z_{5}\right) \, \mathbf{a}_{3}& =&\left(\frac12 + x_{5}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - y_{5}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac14 - z_{5}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{Si II} \\ \mathbf{B}_{35} & =&y_{5} \, \mathbf{a}_{1}+ x_{5} \, \mathbf{a}_{2}- z_{5} \, \mathbf{a}_{3}& =&y_{5} \, a \, \mathbf{\hat{x}}+ x_{5} \, a \, \mathbf{\hat{y}}- z_{5} \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{Si II} \\ \mathbf{B}_{36} & =&- y_{5} \, \mathbf{a}_{1}- x_{5} \, \mathbf{a}_{2}+ \left(\frac12 - z_{5}\right) \, \mathbf{a}_{3}& =&- y_{5} \, a \, \mathbf{\hat{x}}- x_{5} \, a \, \mathbf{\hat{y}}+ \left(\frac12 - z_{5}\right) \, c \, \mathbf{\hat{z}}& \left(8b\right) & \mbox{Si II} \\ \end{array} \]References
- J. Shropshire, P. P. Keat, and P. A. Vaughan, The crystal structure of keatite, a new form of silica, Zeitschrift für Kristallographie 112, 409–413 (1959), doi:10.1524/zkri.1959.112.1-6.409.
- R. W. G. Wyckoff, Crystal Structures Vol. 1 (Wiley, 1963), 2nd edn.
Found in
- T. Demuth, Y. Jeanvoine, J. Hafner, and J. G. Ángyán, Polymorphism in silica studied in the local density and generalized–gradient approximations, J. Phys. Condens. Matter 11, 3833–3874 (1999), doi:10.1088/0953-8984/11/19/306.