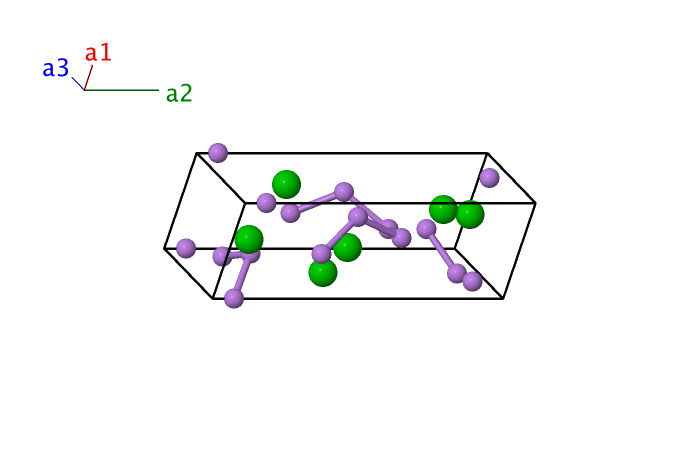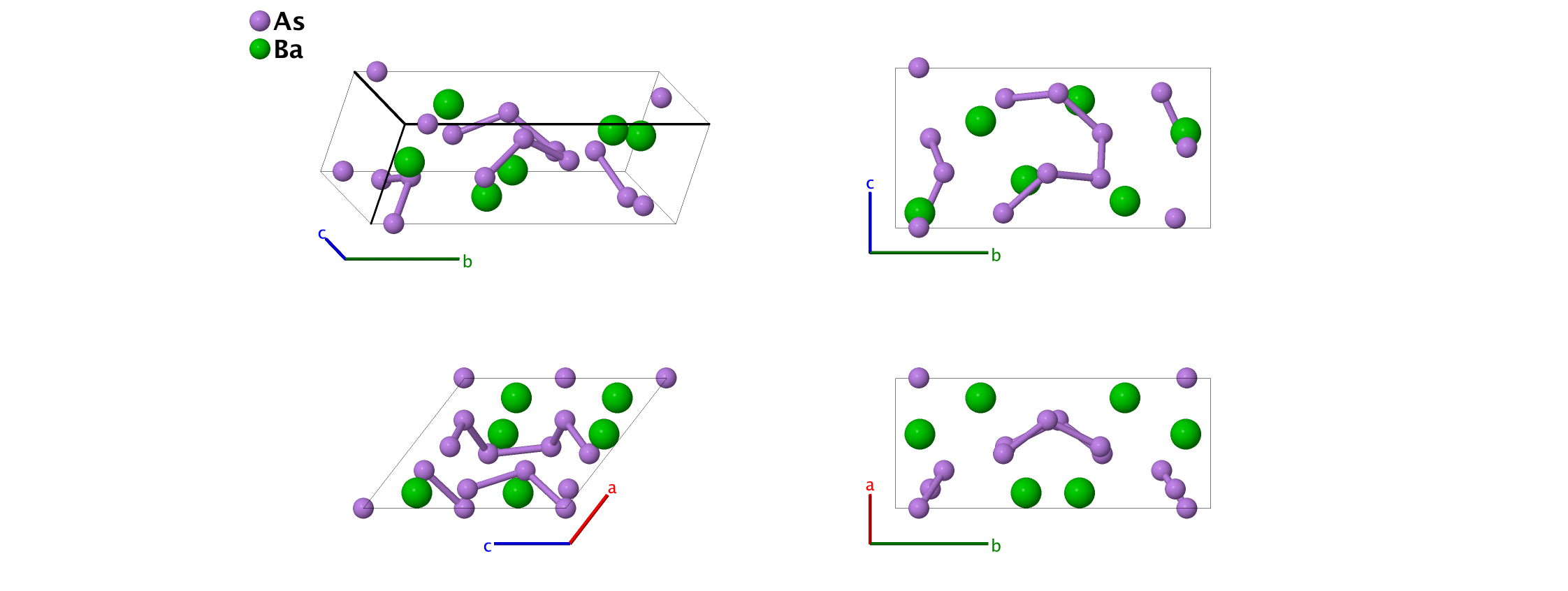
As2Ba Structure: A2B_mP18_7_6a_3a
| Prototype | : | As2Ba |
| AFLOW prototype label | : | A2B_mP18_7_6a_3a |
| Strukturbericht designation | : | None |
| Pearson symbol | : | mP18 |
| Space group number | : | 7 |
| Space group symbol | : | $Pc$ |
| AFLOW prototype command | : | aflow --proto=A2B_mP18_7_6a_3a --params=$a,b/a,c/a,\beta,x_{1},y_{1},z_{1},x_{2},y_{2},z_{2},x_{3},y_{3},z_{3},x_{4},y_{4},z_{4},x_{5},y_{5},z_{5},x_{6}, \\y_{6},z_{6},x_{7},y_{7},z_{7},x_{8},y_{8},z_{8},x_{9},y_{9},z_{9}$ |
Simple Monoclinic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \\
\mathbf{a}_2 & = & b \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \cos\beta \, \mathbf{\hat{x}} + c \sin\beta \, \mathbf{\hat{z}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = & x_{1} \, \mathbf{a}_{1} + y_{1} \, \mathbf{a}_{2} + z_{1} \, \mathbf{a}_{3} & = & \left(x_{1}a+z_{1}c\cos\beta\right) \, \mathbf{\hat{x}} + y_{1}b \, \mathbf{\hat{y}} + z_{1}c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{As I} \\ \mathbf{B}_{2} & = & x_{1} \, \mathbf{a}_{1}-y_{1} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{1}\right) \, \mathbf{a}_{3} & = & \left(\frac{1}{2}c\cos\beta +x_{1}a + z_{1}c\cos\beta\right) \, \mathbf{\hat{x}}-y_{1}b \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{1}\right)c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{As I} \\ \mathbf{B}_{3} & = & x_{2} \, \mathbf{a}_{1} + y_{2} \, \mathbf{a}_{2} + z_{2} \, \mathbf{a}_{3} & = & \left(x_{2}a+z_{2}c\cos\beta\right) \, \mathbf{\hat{x}} + y_{2}b \, \mathbf{\hat{y}} + z_{2}c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{As II} \\ \mathbf{B}_{4} & = & x_{2} \, \mathbf{a}_{1}-y_{2} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{2}\right) \, \mathbf{a}_{3} & = & \left(\frac{1}{2}c\cos\beta +x_{2}a + z_{2}c\cos\beta\right) \, \mathbf{\hat{x}}-y_{2}b \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{2}\right)c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{As II} \\ \mathbf{B}_{5} & = & x_{3} \, \mathbf{a}_{1} + y_{3} \, \mathbf{a}_{2} + z_{3} \, \mathbf{a}_{3} & = & \left(x_{3}a+z_{3}c\cos\beta\right) \, \mathbf{\hat{x}} + y_{3}b \, \mathbf{\hat{y}} + z_{3}c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{As III} \\ \mathbf{B}_{6} & = & x_{3} \, \mathbf{a}_{1}-y_{3} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{3}\right) \, \mathbf{a}_{3} & = & \left(\frac{1}{2}c\cos\beta +x_{3}a + z_{3}c\cos\beta\right) \, \mathbf{\hat{x}}-y_{3}b \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{3}\right)c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{As III} \\ \mathbf{B}_{7} & = & x_{4} \, \mathbf{a}_{1} + y_{4} \, \mathbf{a}_{2} + z_{4} \, \mathbf{a}_{3} & = & \left(x_{4}a+z_{4}c\cos\beta\right) \, \mathbf{\hat{x}} + y_{4}b \, \mathbf{\hat{y}} + z_{4}c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{As IV} \\ \mathbf{B}_{8} & = & x_{4} \, \mathbf{a}_{1}-y_{4} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{4}\right) \, \mathbf{a}_{3} & = & \left(\frac{1}{2}c\cos\beta +x_{4}a + z_{4}c\cos\beta\right) \, \mathbf{\hat{x}}-y_{4}b \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{4}\right)c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{As IV} \\ \mathbf{B}_{9} & = & x_{5} \, \mathbf{a}_{1} + y_{5} \, \mathbf{a}_{2} + z_{5} \, \mathbf{a}_{3} & = & \left(x_{5}a+z_{5}c\cos\beta\right) \, \mathbf{\hat{x}} + y_{5}b \, \mathbf{\hat{y}} + z_{5}c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{As V} \\ \mathbf{B}_{10} & = & x_{5} \, \mathbf{a}_{1}-y_{5} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{5}\right) \, \mathbf{a}_{3} & = & \left(\frac{1}{2}c\cos\beta +x_{5}a + z_{5}c\cos\beta\right) \, \mathbf{\hat{x}}-y_{5}b \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{5}\right)c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{As V} \\ \mathbf{B}_{11} & = & x_{6} \, \mathbf{a}_{1} + y_{6} \, \mathbf{a}_{2} + z_{6} \, \mathbf{a}_{3} & = & \left(x_{6}a+z_{6}c\cos\beta\right) \, \mathbf{\hat{x}} + y_{6}b \, \mathbf{\hat{y}} + z_{6}c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{As VI} \\ \mathbf{B}_{12} & = & x_{6} \, \mathbf{a}_{1}-y_{6} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{6}\right) \, \mathbf{a}_{3} & = & \left(\frac{1}{2}c\cos\beta +x_{6}a + z_{6}c\cos\beta\right) \, \mathbf{\hat{x}}-y_{6}b \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{6}\right)c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{As VI} \\ \mathbf{B}_{13} & = & x_{7} \, \mathbf{a}_{1} + y_{7} \, \mathbf{a}_{2} + z_{7} \, \mathbf{a}_{3} & = & \left(x_{7}a+z_{7}c\cos\beta\right) \, \mathbf{\hat{x}} + y_{7}b \, \mathbf{\hat{y}} + z_{7}c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{Ba I} \\ \mathbf{B}_{14} & = & x_{7} \, \mathbf{a}_{1}-y_{7} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{7}\right) \, \mathbf{a}_{3} & = & \left(\frac{1}{2}c\cos\beta +x_{7}a + z_{7}c\cos\beta\right) \, \mathbf{\hat{x}}-y_{7}b \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{7}\right)c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{Ba I} \\ \mathbf{B}_{15} & = & x_{8} \, \mathbf{a}_{1} + y_{8} \, \mathbf{a}_{2} + z_{8} \, \mathbf{a}_{3} & = & \left(x_{8}a+z_{8}c\cos\beta\right) \, \mathbf{\hat{x}} + y_{8}b \, \mathbf{\hat{y}} + z_{8}c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{Ba II} \\ \mathbf{B}_{16} & = & x_{8} \, \mathbf{a}_{1}-y_{8} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{8}\right) \, \mathbf{a}_{3} & = & \left(\frac{1}{2}c\cos\beta +x_{8}a + z_{8}c\cos\beta\right) \, \mathbf{\hat{x}}-y_{8}b \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{8}\right)c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{Ba II} \\ \mathbf{B}_{17} & = & x_{9} \, \mathbf{a}_{1} + y_{9} \, \mathbf{a}_{2} + z_{9} \, \mathbf{a}_{3} & = & \left(x_{9}a+z_{9}c\cos\beta\right) \, \mathbf{\hat{x}} + y_{9}b \, \mathbf{\hat{y}} + z_{9}c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{Ba III} \\ \mathbf{B}_{18} & = & x_{9} \, \mathbf{a}_{1}-y_{9} \, \mathbf{a}_{2} + \left(\frac{1}{2} +z_{9}\right) \, \mathbf{a}_{3} & = & \left(\frac{1}{2}c\cos\beta +x_{9}a + z_{9}c\cos\beta\right) \, \mathbf{\hat{x}}-y_{9}b \, \mathbf{\hat{y}} + \left(\frac{1}{2} +z_{9}\right)c\sin\beta \, \mathbf{\hat{z}} & \left(2a\right) & \mbox{Ba III} \\ \end{array} \]References
- F. Emmerling, D. Petri, and C. Röhr, Neue Arsenide mit As––Ketten und –Ringen: BaAs2 und AIBa2As5 (AI = K, Rb), Z. Anorg. Allg. Chem. 630, 2490–2501 (2004), doi:10.1002/zaac.200400257.
Found in
- P. Villars and K. Cenzual, Pearson's Crystal Data – Crystal Structure Database for Inorganic Compounds, ASM International (2013).