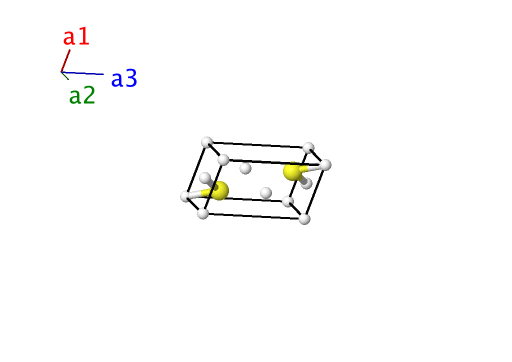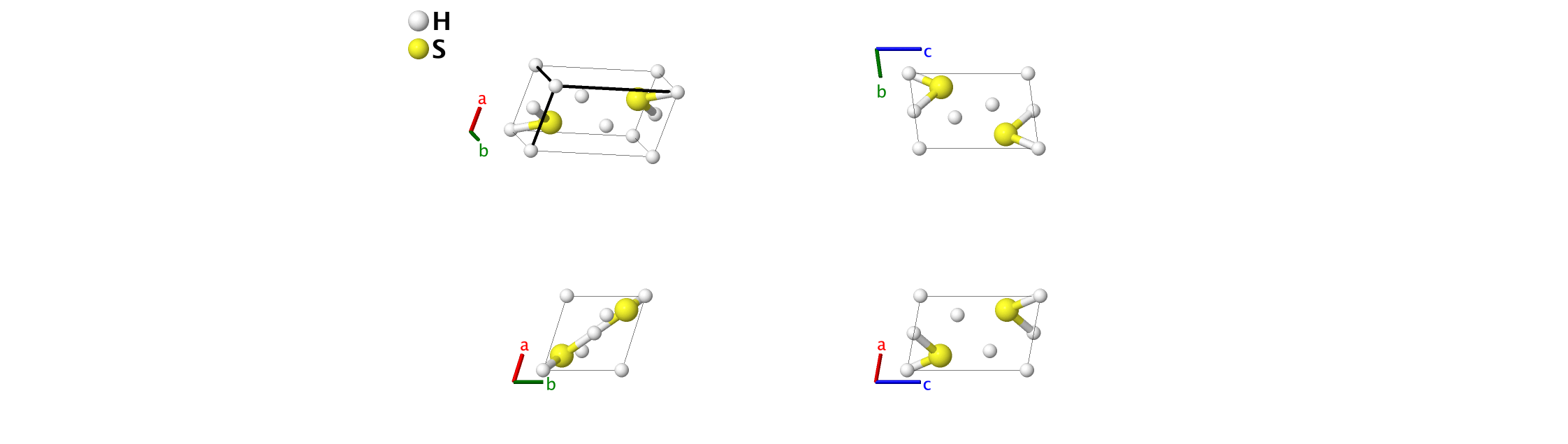
H2S (90 GPa) Structure: A2B_aP6_2_aei_i
| Prototype | : | H2S |
| AFLOW prototype label | : | A2B_aP6_2_aei_i |
| Strukturbericht designation | : | None |
| Pearson symbol | : | aP6 |
| Space group number | : | 2 |
| Space group symbol | : | $P\bar{1}$ |
| AFLOW prototype command | : | aflow --proto=A2B_aP6_2_aei_i --params=$a,b/a,c/a,\alpha,\beta,\gamma,x_{3},y_{3},z_{3},x_{4},y_{4},z_{4}$ |
- This structure was found by first-principles electronic structure calculations and is predicted to be the stable structure of H2S in the range $80 - 140 GPa. The data presented here was computed at 90 GPa. The original reference places H atoms on (1g), (1f) and (2i) sites, with S atoms on (2i) sites. We have changed the origin so that the H atoms are now on (1a), (1e) and (2i) sites.
Triclinic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & a \mathbf{\hat{x}} \\
\mathbf{a}_2 & = & b \cos\gamma \, \mathbf{\hat{x}} + b \sin\gamma \,\mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c_x \mathbf{\hat{x}} + c_y \, \mathbf{\hat{y}} + c_z \, \mathbf{\hat{z}}\\\\
c_x & = & c \, \cos\beta \\
c_y & = & c \, (\cos\alpha -\cos\beta \cos\gamma)/\sin\gamma \\
c_z & = & \sqrt{c^2-c_x^2-c_y^2}
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = & 0 \, \mathbf{a}_{1} + 0 \, \mathbf{a}_{2} + 0 \, \mathbf{a}_{3} & = & 0 \, \mathbf{\hat{x}} + 0 \, \mathbf{\hat{y}} + 0 \, \mathbf{\hat{z}} & \left(1a\right) & \mbox{H I} \\ \mathbf{B}_{2} & = & \frac{1}{2} \, \mathbf{a}_{1} + \frac{1}{2} \, \mathbf{a}_{2} & = & \frac{1}{2}\left(a+b\cos\gamma\right) \, \mathbf{\hat{x}} + \frac{1}{2}b\sin\gamma \, \mathbf{\hat{y}} & \left(1e\right) & \mbox{H II} \\ \mathbf{B}_{3} & = & x_{3} \, \mathbf{a}_{1} + y_{3} \, \mathbf{a}_{2} + z_{3} \, \mathbf{a}_{3} & = & \left(x_{3}a+y_{3}b\cos\gamma+z_{3}c_{x}\right) \, \mathbf{\hat{x}} + \left(y_{3}b\sin\gamma+z_{3}c_{y}\right) \, \mathbf{\hat{y}} + z_{3}c_{z} \, \mathbf{\hat{z}} & \left(2i\right) & \mbox{H III} \\ \mathbf{B}_{4} & = & -x_{3} \, \mathbf{a}_{1}-y_{3} \, \mathbf{a}_{2}-z_{3} \, \mathbf{a}_{3} & = & \left(-x_{3}a-y_{3}b\cos\gamma-z_{3}c_{x}\right) \, \mathbf{\hat{x}} + \left(-y_{3}b\sin\gamma-z_{3}c_{y}\right) \, \mathbf{\hat{y}}-z_{3}c_{z} \, \mathbf{\hat{z}} & \left(2i\right) & \mbox{H III} \\ \mathbf{B}_{5} & = & x_{4} \, \mathbf{a}_{1} + y_{4} \, \mathbf{a}_{2} + z_{4} \, \mathbf{a}_{3} & = & \left(x_{4}a+y_{4}b\cos\gamma+z_{4}c_{x}\right) \, \mathbf{\hat{x}} + \left(y_{4}b\sin\gamma+z_{4}c_{y}\right) \, \mathbf{\hat{y}} + z_{4}c_{z} \, \mathbf{\hat{z}} & \left(2i\right) & \mbox{S} \\ \mathbf{B}_{6} & = & -x_{4} \, \mathbf{a}_{1}-y_{4} \, \mathbf{a}_{2}-z_{4} \, \mathbf{a}_{3} & = & \left(-x_{4}a-y_{4}b\cos\gamma-z_{4}c_{x}\right) \, \mathbf{\hat{x}} + \left(-y_{4}b\sin\gamma-z_{4}c_{y}\right) \, \mathbf{\hat{y}}-z_{4}c_{z} \, \mathbf{\hat{z}} & \left(2i\right) & \mbox{S} \\ \end{array} \]References
- Y. Li, J. Hao, H. Liu, Y. Li, and Y. Ma, The metallization and superconductivity of dense hydrogen sulfide, J. Chem. Phys. 140, 174712 (2014), doi:10.1063/1.4874158.