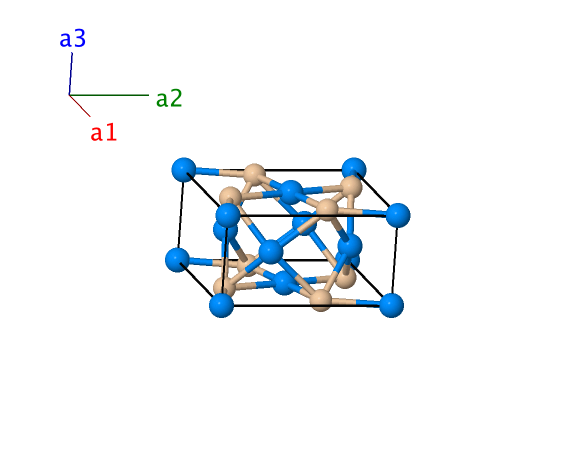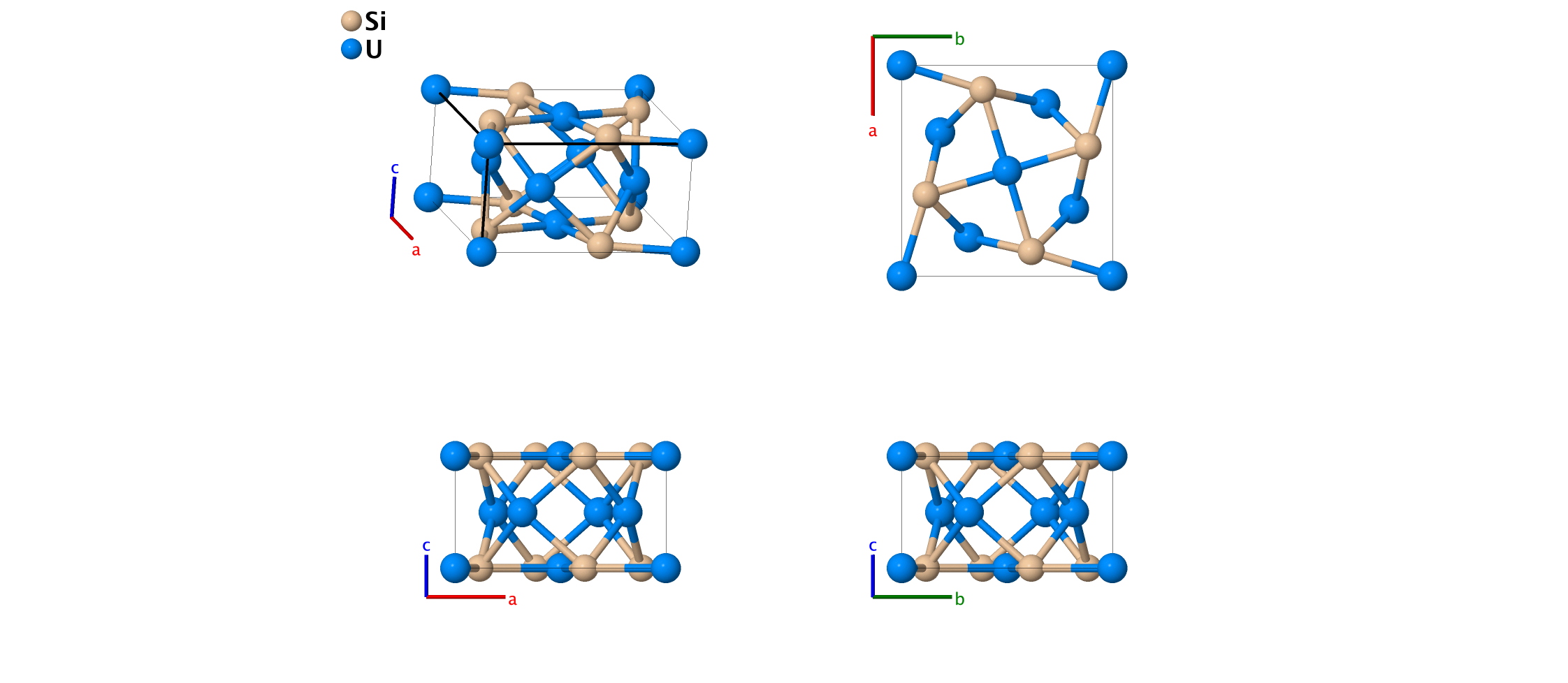
Si2U3 (D5a) Structure: A2B3_tP10_127_g_ah
| Prototype | : | Si2U3 |
| AFLOW prototype label | : | A2B3_tP10_127_g_ah |
| Strukturbericht designation | : | $D5_{a}$ |
| Pearson symbol | : | tP10 |
| Space group number | : | 127 |
| Space group symbol | : | $\mbox{P4/mbm}$ |
| AFLOW prototype command | : | aflow --proto=A2B3_tP10_127_g_ah --params=$a,c/a,x_{2},x_{3}$ |
- If we consider the Si2 dimers as a pseudo-atom, then this is a tetragonal distortion of the Cu3Au (L12) structure.
Simple Tetragonal primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & a \, \mathbf{\hat{x}} \\
\mathbf{a}_2 & = & a \, \mathbf{\hat{y}} \\
\mathbf{a}_3 & = & c \, \mathbf{\hat{z}}\\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & =&0 \, \mathbf{a}_{1} + 0 \, \mathbf{a}_{2} + 0 \, \mathbf{a}_{3} & =&0 \mathbf{\hat{x}} + 0 \mathbf{\hat{y}} + 0 \mathbf{\hat{z}} & \left(2a\right) & \mbox{U I} \\ \mathbf{B}_{2} & =&\frac12 \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{2}& =&\frac12 \, a \, \mathbf{\hat{x}}+ \frac12 \, a \, \mathbf{\hat{y}}& \left(2a\right) & \mbox{U I} \\ \mathbf{B}_{3} & =&x_{2} \, \mathbf{a}_{1}+ \left(\frac12 + x_{2}\right) \, \mathbf{a}_{2}& =&x_{2} \, a \, \mathbf{\hat{x}}+ \left(\frac12 + x_{2}\right) \, a \, \mathbf{\hat{y}}& \left(4g\right) & \mbox{Si} \\ \mathbf{B}_{4} & =&- x_{2} \, \mathbf{a}_{1}+ \left(\frac12 - x_{2}\right) \, \mathbf{a}_{2}& =&- x_{2} \, a \, \mathbf{\hat{x}}+ \left(\frac12 - x_{2}\right) \, a \, \mathbf{\hat{y}}& \left(4g\right) & \mbox{Si} \\ \mathbf{B}_{5} & =&\left(\frac12 - x_{2}\right) \, \mathbf{a}_{1}+ x_{2} \, \mathbf{a}_{2}& =&\left(\frac12 - x_{2}\right) \, a \, \mathbf{\hat{x}}+ x_{2} \, a \, \mathbf{\hat{y}}& \left(4g\right) & \mbox{Si} \\ \mathbf{B}_{6} & =&\left(\frac12 + x_{2}\right) \, \mathbf{a}_{1}- x_{2} \, \mathbf{a}_{2}& =&\left(\frac12 + x_{2}\right) \, a \, \mathbf{\hat{x}}- x_{2} \, a \, \mathbf{\hat{y}}& \left(4g\right) & \mbox{Si} \\ \mathbf{B}_{7} & =&x_{3} \, \mathbf{a}_{1}+ \left(\frac12 + x_{3}\right) \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& =&x_{3} \, a \, \mathbf{\hat{x}}+ \left(\frac12 + x_{3}\right) \, a \, \mathbf{\hat{y}}+ \frac12 \, c \, \mathbf{\hat{z}}& \left(4h\right) & \mbox{U II} \\ \mathbf{B}_{8} & =&- x_{3} \, \mathbf{a}_{1}+ \left(\frac12 - x_{3}\right) \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& =&- x_{3} \, a \, \mathbf{\hat{x}}+ \left(\frac12 - x_{3}\right) \, a \, \mathbf{\hat{y}}+ \frac12 \, c \, \mathbf{\hat{z}}& \left(4h\right) & \mbox{U II} \\ \mathbf{B}_{9} & =&\left(\frac12 - x_{3}\right) \, \mathbf{a}_{1}+ x_{3} \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& =&\left(\frac12 - x_{3}\right) \, a \, \mathbf{\hat{x}}+ x_{3} \, a \, \mathbf{\hat{y}}+ \frac12 \, c \, \mathbf{\hat{z}}& \left(4h\right) & \mbox{U II} \\ \mathbf{B}_{10} & =&\left(\frac12 + x_{3}\right) \, \mathbf{a}_{1}- x_{3} \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& =&\left(\frac12 + x_{3}\right) \, a \, \mathbf{\hat{x}}- x_{3} \, a \, \mathbf{\hat{y}}+ \frac12 \, c \, \mathbf{\hat{z}}& \left(4h\right) & \mbox{U II} \\ \end{array} \]References
- K. Remschnig, T. Le Bihan, H. Noël, and P. Rogl, Structural chemistry and magnetic behavior of binary uranium silicides, J. Solid State Chem. 97, 391–399 (1992), doi:10.1016/0022-4596(92)90048-Z.
Found in
- P. Villars, K. Cenzual, R. Gladyshevskii, O. Shcherban, V. Dubenskyy, V. Kuprysyuk, I. Savesyuk, and R. Zaremba, Landolt–Börnstein – Group III Condensed Matter (Springer–Verlag GmbH, Heidelberg, 2012). Accessed through the Springer Materials site.