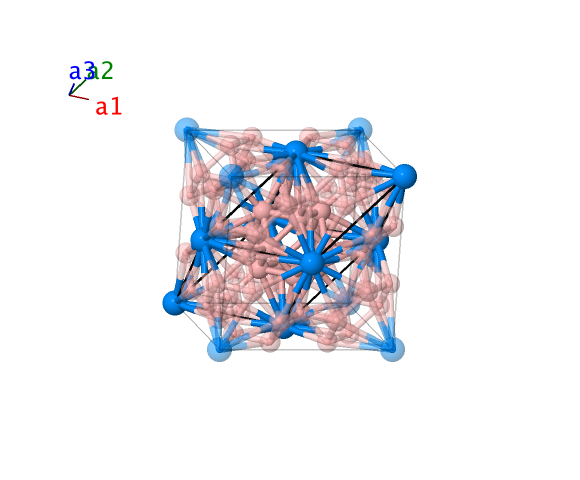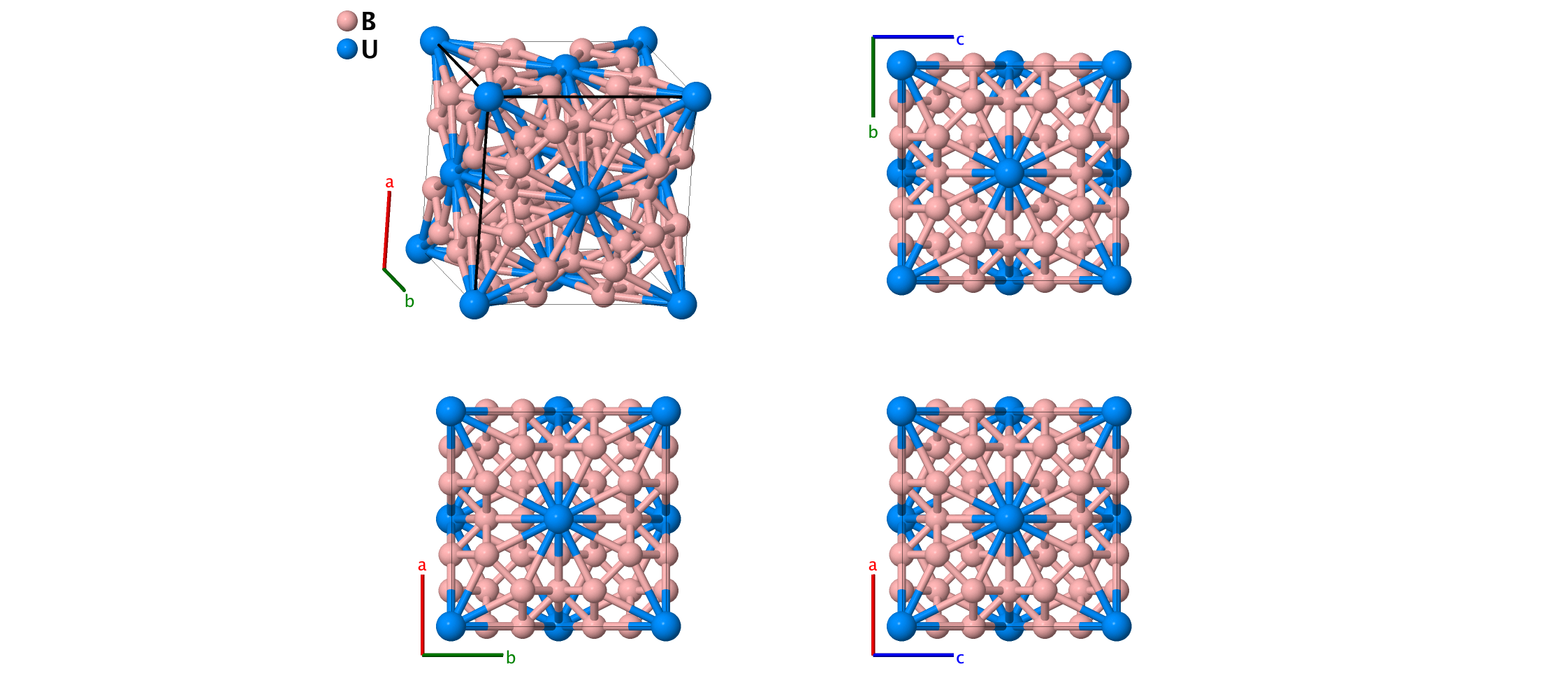
UB12 ($D2_{f}$) Structure: A12B_cF52_225_i_a
| Prototype | : | UB12 |
| AFLOW prototype label | : | A12B_cF52_225_i_a |
| Strukturbericht designation | : | $D2_{f}$ |
| Pearson symbol | : | cF52 |
| Space group number | : | 225 |
| Space group symbol | : | $\mbox{Fm}\bar{3}\mbox{m}$ |
| AFLOW prototype command | : | aflow --proto=A12B_cF52_225_i_a --params=$a,y_{2}$ |
Other compounds with this structure
- DyB12, ErB12, LuB12, ThB12, TmB12, YB12, YbB12, ZrB12, and (Th0.93Zr0.07)B12
Face-centered Cubic primitive vectors:
\[
\begin{array}{ccc}
\mathbf{a}_1 & = & \frac12 \, a \, \mathbf{\hat{y}} + \frac12 \, a \, \mathbf{\hat{z}} \\
\mathbf{a}_2 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, a \, \mathbf{\hat{z}} \\
\mathbf{a}_3 & = & \frac12 \, a \, \mathbf{\hat{x}} + \frac12 \, a \, \mathbf{\hat{y}} \\
\end{array}
\]
Basis vectors:
\[ \begin{array}{ccccccc} & & \mbox{Lattice Coordinates} & & \mbox{Cartesian Coordinates} &\mbox{Wyckoff Position} & \mbox{Atom Type} \\ \mathbf{B}_{1} & = &0 \, \mathbf{a}_{1} + 0 \, \mathbf{a}_{2} + 0 \, \mathbf{a}_{3} & = &0 \mathbf{\hat{x}} + 0 \mathbf{\hat{y}} + 0 \mathbf{\hat{z}} & \left(4a\right) & \mbox{U} \\ \mathbf{B}_{2} & = &\left(\frac12 + 2 \, y_{2}\right) \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\hat{x}}+ \left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{z}}& \left(48i\right) & \mbox{B} \\ \mathbf{B}_{3} & = &\frac12 \, \mathbf{a}_{1}+ \left(\frac12 + 2 \, y_{2}\right) \, \mathbf{a}_{2}+ \left(\frac12 - 2 \, y_{2}\right) \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\hat{x}}+ \left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{z}}& \left(48i\right) & \mbox{B} \\ \mathbf{B}_{4} & = &\frac12 \, \mathbf{a}_{1}+ \left(\frac12 - 2 \, y_{2}\right) \, \mathbf{a}_{2}+ \left(\frac12 + 2 \, y_{2}\right) \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\hat{x}}+ \left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{z}}& \left(48i\right) & \mbox{B} \\ \mathbf{B}_{5} & = &\left(\frac12 - 2 \, y_{2}\right) \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& = &\frac12 \, a \, \mathbf{\hat{x}}+ \left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{y}}+ \left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{z}}& \left(48i\right) & \mbox{B} \\ \mathbf{B}_{6} & = &+ \frac12 \, \mathbf{a}_{1}+ \left(\frac12 + 2 \, y_{2}\right) \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& = &\left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{x}}+ \frac12 \, a \, \mathbf{\hat{y}}+ \left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{z}}& \left(48i\right) & \mbox{B} \\ \mathbf{B}_{7} & = &\left(\frac12 - 2 \, y_{2}\right) \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{2}+ \left(\frac12 + 2 \, y_{2}\right) \, \mathbf{a}_{3}& = &\left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{x}}+ \frac12 \, a \, \mathbf{\hat{y}}\left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{z}}& \left(48i\right) & \mbox{B} \\ \mathbf{B}_{8} & = &\left(\frac12 + 2 \, y_{2}\right) \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{2}+ \left(\frac12 - 2 \, y_{2}\right) \, \mathbf{a}_{3}& = &\left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{x}}+ \frac12 \, a \, \mathbf{\hat{y}}+ \left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{z}}& \left(48i\right) & \mbox{B} \\ \mathbf{B}_{9} & = &\frac12 \, \mathbf{a}_{1}+ \left(\frac12 - 2 \, y_{2}\right) \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& = &\left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{x}}+ \frac12 \, a \, \mathbf{\hat{y}}\left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{z}}& \left(48i\right) & \mbox{B} \\ \mathbf{B}_{10} & = &\frac12 \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{2}+ \left(\frac12 + 2 \, y_{2}\right) \, \mathbf{a}_{3}& = &\left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{y}}+ \frac12 \, a \, \mathbf{\hat{z}}& \left(48i\right) & \mbox{B} \\ \mathbf{B}_{11} & = &\left(\frac12 + 2 \, y_{2}\right) \, \mathbf{a}_{1}+ \left(\frac12 - 2 \, y_{2}\right) \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& = &\left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{y}}+ \frac12 \, a \, \mathbf{\hat{z}}& \left(48i\right) & \mbox{B} \\ \mathbf{B}_{12} & = &\left(\frac12 - 2 \, y_{2}\right) \, \mathbf{a}_{1}+ \left(\frac12 + 2 \, y_{2}\right) \, \mathbf{a}_{2}+ \frac12 \, \mathbf{a}_{3}& = &\left(\frac12 + y_{2}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{y}}+ \frac12 \, a \, \mathbf{\hat{z}}& \left(48i\right) & \mbox{B} \\ \mathbf{B}_{13} & = &\frac12 \, \mathbf{a}_{1}+ \frac12 \, \mathbf{a}_{2}+ \left(\frac12 - 2 \, y_{2}\right) \, \mathbf{a}_{3}& = &\left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{x}}+ \left(\frac12 - y_{2}\right) \, a \, \mathbf{\hat{y}}+ \frac12 \, a \, \mathbf{\hat{z}}& \left(48i\right) & \mbox{B} \\ \end{array} \]References
- P. Blum and F. Bertaut, Contribution ‘a l’Étude des Borures ‘a Teneur Élevée en Bore, Acta Cryst. 7, 81–86 (1954), doi:10.1107/S0365110X54000151.
Found in
- W. B. Pearson, The Crystal Chemistry and Physics of Metals and Alloys (Wiley– Interscience, New York, London, Sydney, Toronto, 1972)., pp. 757-759.